لا يوجد طالب علم لا يعرف فيثاغورس ، هذا الفيلسوف اليوناني وعالم الرياضيات المولود بعام 570 قبل الميلاد بمدينة ساموس باليونان ، وتتراوح المدة التي توفي فيها فيثاغورس ما بين العام 500 والعام 490 ق.م بمنطقة لوكانيا بمدينة إيطاليا ، وقد أسس العالم هذا الفيثاغورية ، وبالرغم من طبيعتها الدينية إلا أن هذه الفيثاغورية وضعت مبادئاً تؤثر على فكر العديد من العلماء والفلاسفة مثل أفلاطون وأرسطو ، كما أنها ساعدت في تطوير علم الرياضيات ذلك بالإضافة للفلسفة العقلانية الغربية ، واشتهر فيثاغورس بوضع مبدا الرياضيات الشهير الذي أطلق عليه (نظرية فيثاغورس) ، واليوم سوف نتعرف على نظريته وسوف نتعرف أيضاً على حياته وإسهاماته العلمية.
حياة العالم فيثاغورس:
- ليس هناك العديد من المعلومات حول حياة العالم فيثاغورس المبكرة ، إلا أن هناك دلائل تشير لأنه كان فرداً من المؤهلين علمياً بشكل جيد ، بالإضافة إلى أنه تعلم كيف يقرأ وكيف يعزف على آلة القيثارة ، وقد زار فيثاغورس مدينة ميليتس وذلك في أواخر سنوات المراهقة من أجل الدراسة مع الفيلسوف طاليس ، وهو رجل مسن ، وكان أناكسيماندر وذلك الرجل كان أحد طلاب طاليس يعطي المحاضرات في المدينة ، ومن المرجح أن يكون فيثاغورس حضر تلك المحاضرات ، وقد اهتم هذا الطالب بعلوم كثيرة مثل علم الهندسة والكونيات ، هذا الأمر قد أثر عليه في فترة الشباب.
- أما بالنسبة للفترة اللاحقة من حياته فقد تبدو غريبة بعض الشيء ، فقد ذهب فيثاغورس لمصر من أجل قضاء الوقت والزيارة ، أو أنه قد حاول أن يذهب للمعابد ، وعندما زار فيثاغورس ديوسبوليس تم قبوله بعد أن تم الانتهاء من الإجراءات اللازمة من أجل متابعة تعليمه في الرياضيات وعلم الهندسة ، هذا الأمر قد ساعده في وضع نظريته الشهيرة.
للمزيد يمكنك قراءة : طرق حفظ جدول الضرب
نظرية فيثاغورس:
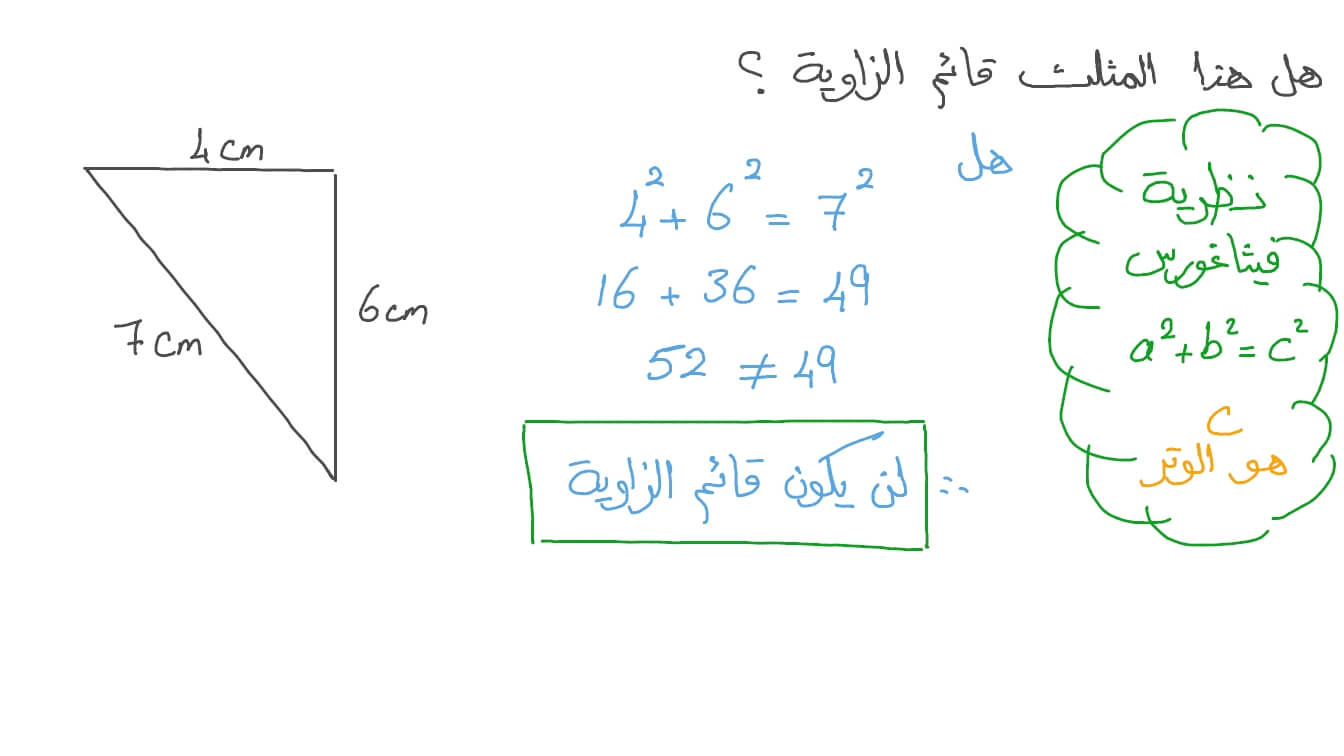
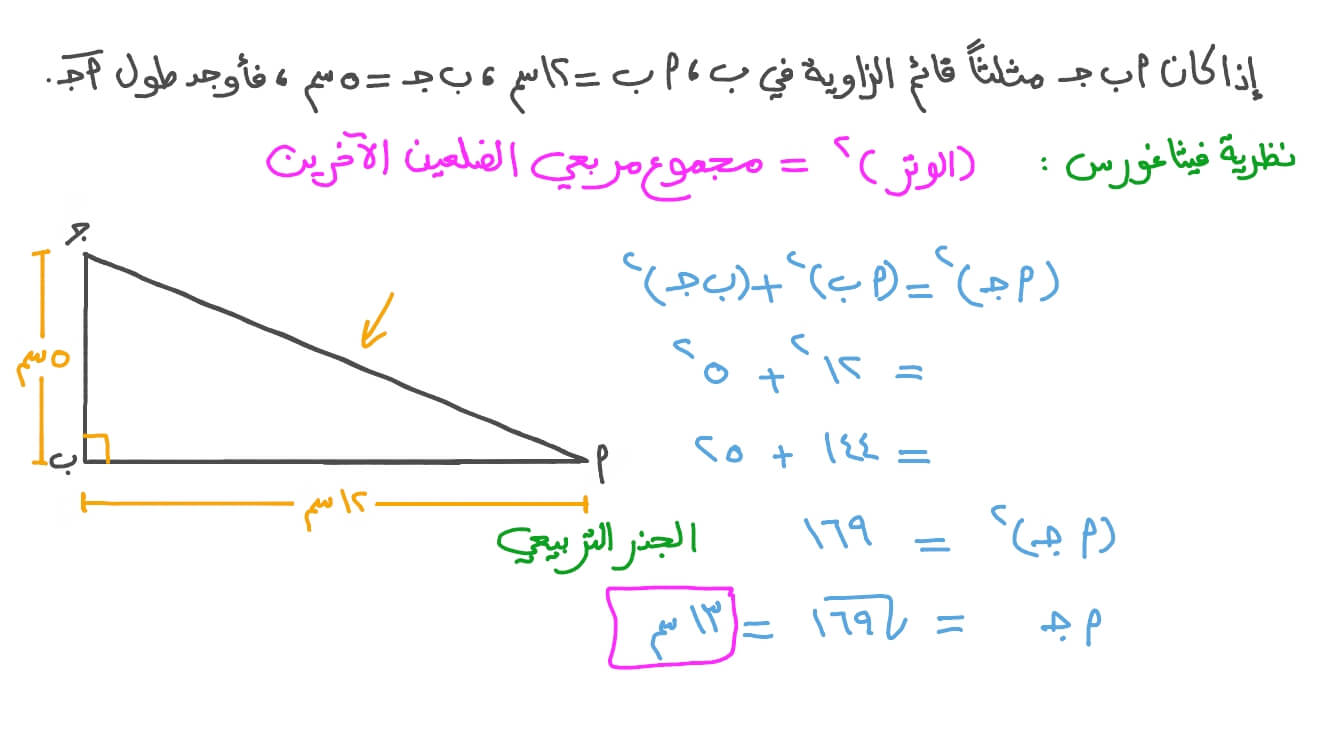
- إن نظرية العالم فيثاغورس تشير للنظرية الرياضيها التي وضعها حيث تنص على أن (مربع وتر المثلث في المثلث القائم الزاوية يساوي مجموع مربعي الجهات الأخرى من المثلث) وبإمكاننا الإشارة إليها رياضياً (ج^2) = (أ^2) + (ب^2) ، حيث تستعمل تلك المعادلة ثلاثة حروف ويتم تطبيقها على مثلث قائم الزاوية فقط ، وهو المثلث الذي يحوي زاوية قائمة واحدة تقاس تسعون درجة ، وعند وجود مثلث قائم الزاوية بالإمكان تسمية جهاته بالحروف المناسبة.
- وفي الغالب يشار لوتر المثلث بالحرف (ج) ، ويشير الوتر للجهة المعاكسة بالاتجاه للزاوية القائمة ويعتبر أطول جهة ، أما بالنسبة للحروف الأخرى وهي (أ ، و ، ب) فهي الجهات الأخرى ولا يعتبر الترتيب مهم بتسميتها ، ولكن عليك أن تنتبه لعدم الخلط بينهما لاحقاً.
براهين نظرية فيثاغورس:
- لقد لاقت نظريته استحسان كبير من الناس حول العالم وذلك لما يقارب الأربعة آلاف عام ، وقد أسهم الكثير من العلماء في البحث عن الدلالات والبراهين على صحة ودعم النظرية ، فقد بلغ العدد التقريبي للبراهين المرتبطة بتلك النظرية ليومنها هذا حوالي 367 برهان ، وكل برهان منهم يختلف عن الآخر ، ومنها برهان مقدم من العالم الكبير بابوس الاسكندري ، بالإضافة لبرهان صادر من العالم العربي ثابت بن قرة ، والفنان الشهير ليوناردو دافنشي ، بالإضافة لرئيس الولايات المتحدة الأمريكية جيمس غارفيلد ، وغيرهم من الشخصيات.
للمزيد يمكنك قراءة : ما هو قانون مساحة المستطيل
إسهامات فيثاغورس:
يرى العديد من العلماء بأن فيثاغورس وتلاميذه لم يدرسوا علم الرياضيات من أجل الدواع والأسباب التي يدركها الناس في الوقت الحالي ، فقد كان للأرقام عند هؤلاء العلماء معاني روحية ، فقد كان يعتقد فيثاغورس بأن كل شيء في هذا الكون عبارة عن أرقام ، وهناك الكثير من النظريات التي يرجع فضلها لفيثاغورس ، وتعتبر نظريته هي النظرية الأشهر بالعالم ، إلا أن تلك النظرية لا تعزى له وحده ، فقد لاحظ البابليون المعلومات التي تدور حول تلك النظرية قبل آلاف السنين من العالم فيثاغورس ، وبالإضافة لإسهاماته بعلم الرياضيات فقد عمل بعلم الفلك كذلك ، وفيما يلي إسهاماته وأفكاره بهذا المجال :
- لقد اعتقد بأن الشكل الكروي هو الشكل المثالي.
- لقد خلص إلى أن النجم المسائي الزهرة هو أيضاً النجم الصباحي.
- لقد أدرك فيثاغورس بأن مدار القمر مائلاً لخط الاستواء الخاص بالكرة الأرضية.
لقد ألهمت أعمال فيثاغورس الكثير من علماء الفلك مثل العالم يوهانس كيبلر وبطليموس اللذين صاغا قوانين حركة الكواكب لاحقاً.
للمزيد يمكنك قراءة : بحث عن علم الرياضيات