من الممكن أن نعرف اللوغاريتمات على أنها العملية العكسية للأسس كما هو الحال بالنسبة للطرح المعروف بالعملية العكسية للجمع ، والقسمة المعروفة بالعملية العكسية للضرب ، واليوم سوف نلقي نظرة عامة حول اللوغاريتمات ، بالإضافة إلى أننا سنتعرف على خصائص اللوغاريتمات ، وغيرها من المعلومات المتعلقة باللوغاريتمات ، فتابعوا معنا.
نظرة عامة حول اللوغاريتمات:
من أجل توضيح أن اللوغاريتم يعد العملية العكسية للأسس إليك المثال التالي : عند رفع العدد اثنين للقوة أربعة فإن الناتج يساوي ستة عشر ، أي 24=16 ، وتعالى نفترض طرح السؤال الآتي : ما هو الأس الذي أساسه العدد اثنين ، ويعطينا ناتجاً يساوي ستة عشر ، فالجواب سوف يكون أربعة ، وذلك ما يتم التعبير عن باستعمال اللوغاريتمات كما يأتي : لو2 16 = 4 ، وعليه فإن 24= 16 ↔ لو2 16 = 4، ويلاحظ من السابق بأن المعادلتين تصف العلاقة ذاتها بين الأعداد اثنين وأربعة وستة عشر ، حيث العدد اثنين هو الأساس ، والعدد أربعة هو الأس ، والعدد ستة عشر هو الناتج ، ومن الممكن توضيح هذا الأمر بشكل أكبر من خلال تقديم سلسلة أخرى من الأمثلة على المعادلة الأسية والمعادلة اللوغاريتمية:
- المعادلة اللوغاريتمية : لو2 8 = 3 ↔ المعادلة الأسية 23 = 8
- المعادلة اللوغاريتمية : لو3 81 = 4 ↔ المعادلة الأسية 34 = 81
- المعادلة اللوغاريتمية : لو5 25 = 2 ↔ المعادلة الأسية 52 = 25
بصورة عامة فإن الشكل العام للمعادلة اللوغاريتمية هي كما يأتي :
لو كانت المعادلة الأسية على شكل ب س = أ ، فإن المعادلة اللوغاريتمية سوف تكون على شكل : لوب أ =س ، إذ :
- ب : الأساس.
- س : الأس.
- أ : الناتج.
نشير هنا إلى أن هناك طرق كثيرة لقراءة اللوغاريتم ، فعلى سبيل المثال من الممكن قراءة اللوغاريتم الآتي بطرق كثيرة : لو2 8 = 3
- لوغاريتم العدد ثمانية للأساس اثنين يساوي ثلاثة.
- لوغاريتم الأساس اثنين لعدد ثمانية يساوي ثلاثة.
- لو كان الأساس اثنين فإن لوغاريتم العدد ثمانية يساوي ثلاثة.
للمزيد يمكنك قراءة : اسئلة ذكاء حسابية
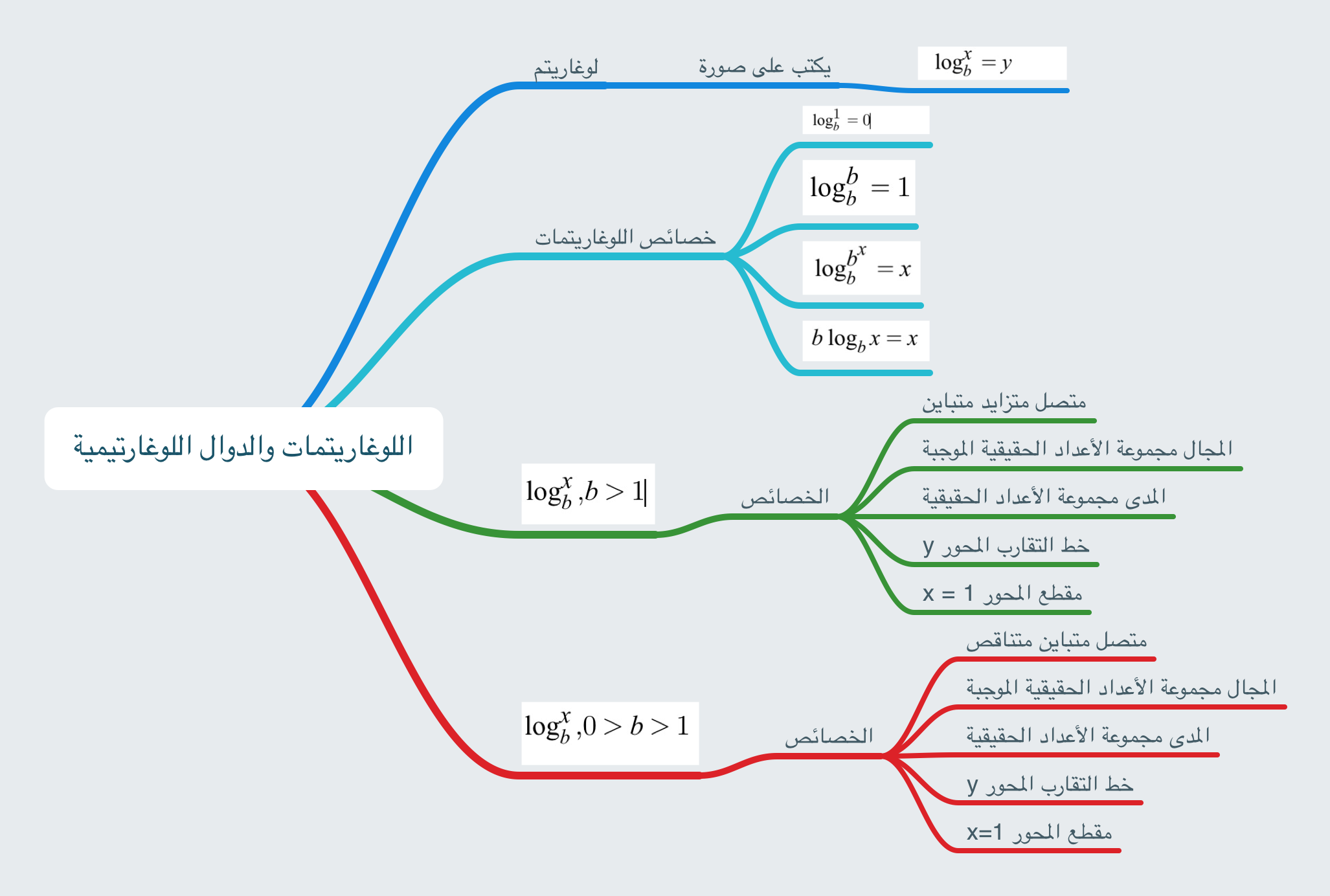
خصائص اللوغاريتمات:
إن اللوغاريتمات تتميز بالخصائص التالية (إذ ب في كل الخصائص هي أساس اللوغاريتم).
- لوب 1 = 0، وهذا لأن رفع أي عدد للقوة صفر يساوي واحد ؛ بمعنى أن: ب 0 = 1.
- لوب ب = 1، وهذا لأن رفع أي عدد للقوة واحد يساوي العدد ذاته ؛ بمعنى أن: ب 1 = ب.
- لوب ب س = س، وبصورة عامة فإنّ: لو ب ب ق (س) = ق (س).
- ب لوب س= س، وبصورة عامة فإنّ: ب لو ب ق(س) = ق(س).
- لوب (س×ص) = لوب س + لوب ص.
- لوب (س/ص) = لوب س – لوب ص.
- لوب س ل = ل×لوب س.
- لو كان: لوب س = لوب ص، فإنّ: س = ص.
- لوب (س+ص) لا يساوي لوب س + لوب ص.
- لوب (س-ص) لا يساوي لوب س – لوب ص.
- لوب أ = قيمة غير معرّفة، لو كانت قيمة أ تساوي عدد سالب.
- لوب 0 = قيمة غير معرّفة، وهذا لأنه ليس من الممكن لنتيجة أي عدد عند رفعه لأحد الأسس أن يكون صفر.
إن قلب اللوغاريتم بمعنى جعل مقامه مكان بسطه ، وبسطه مكان مقامه ، أو العكس يؤدي لتبديل الناتج ، والأساس ، وذلك كما يأتي :
- لوب أ = 1/لوأ ب؛ مثل: 5/(2×لوس ص) = (5×لوص س)/2
من الممكن ضرب 2 من اللوغاريتمات ، أو أكثر من اثنين ، وإيجاد الناتج النهائي لحاصل ضربهما بإحدى الحالتين التاليتين فقط :
- الحالة الأولى : لو كان ناتج اللوغاريتم الأول ، وأساس اللوغاريتم الثاني متعادلين.
- الحالة الثانية : لو كان أساس اللوغاريتم الأول ، وناتج اللوغاريتم الثاني متعادلين.
- لينتج أن : لوأ ب× لوب جـ = لوأ جـ.
من الممكن حساب قيمة اللوغاريتمات العشرية والطبيعية باستعمال الآلة الحاسبة ، لهذا من الممكن تغيير أساس اللوغاريتم للعدد النيبيري أو العدد عشرة ؛ من أجل تسهيل عملية حسابه باستعمال الآلة الحاسبة من خلال خاصية تغيير الأساس ، والتي تنص على أن : لوأ س = لوب س/لوب أ؛ حيث ب= 10، أو العدد النيبيري (هـ).
للمزيد يمكنك قراءة : ماذا اخترع اينشتاين
معلومات مصورة عن اللوغاريتمات:

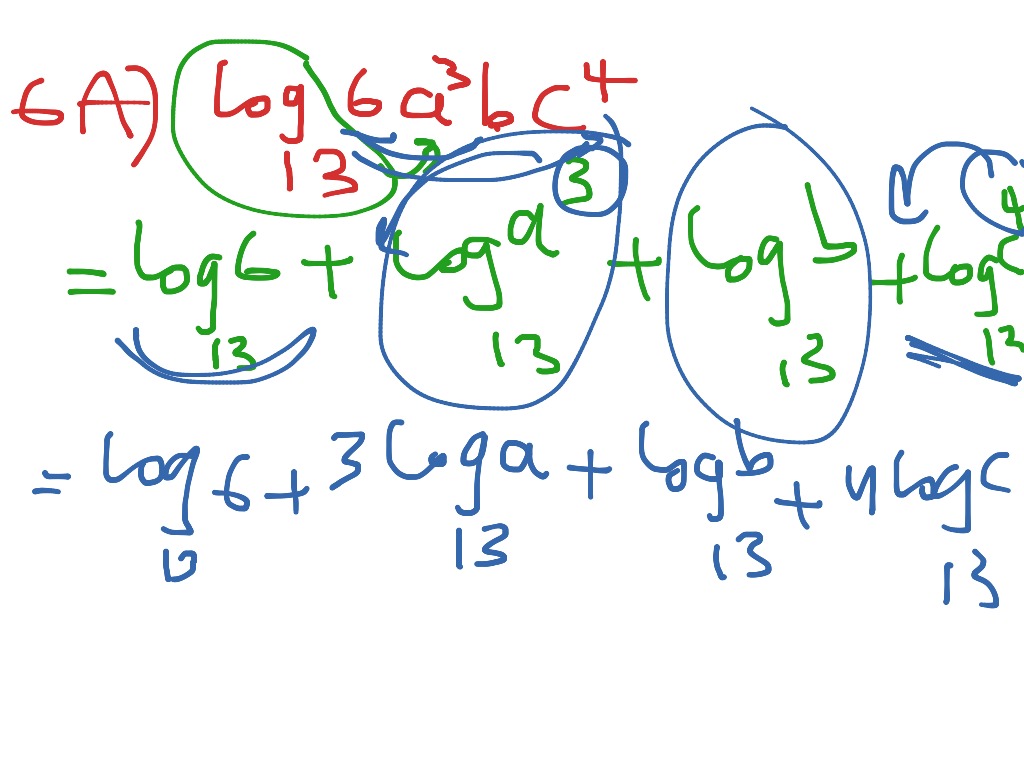
للمزيد يمكنك قراءة : تعريف علم الفيزياء