محتوي الموضوع
الدائرة هي شكل من الأشكال الهندسية المغلقة المتكونة من عدد من النقاط التي وصل فيما بينها بخط منحن مغلق ، فكل نقطة من تلك النقاط تبعد بعد ثابت عن نقطة محددة موجودة داخل الدائرة يطلق عليها المركز ، واليوم سوف نتعرف سوياً عن كيفية حساب محيط الدائرة ، بالإضافة لكيفية إيجاد محيط الدائرة يدوياً ، ومفاهيم هامة تتعلق بالدائرة ، وبعض الأمثلة التي سنوضح فيها كيفية حساب محيط الدائرة ، فتابعوا معنا.
كيفية حساب محيط الدائرة:

- لو أحضرنا 3 دوائر متفاوتة المساحة ، وطُلب منا أن نجد النسبة بين المحيط إلى طول القطر ، بسهولة يتم إيجاد محيط الدائرة باستعمال الطريقة التي ذكرناها سابقاً ، ومن ثم يقسم على طول القطر ، وبعدها يتم تدوين نتيجة كل دائرة وحدها ، وسنلاحظ بعد أن ندون النتائج بأن النسبة بين المحيط إلى القطر ثابتة في جميع الدوائر مهما اختلفت المساحة ، ومن هنا يتبين لنا بأن النسبة بين محيط الدائرة لقطرها ثابتة لا تتغير ، وهي نسبة تقريبية ، وهي تساوي تقريباً 3.14 أو 7/22 ، ويتم الرمز إليها بـ(π) وتقرأ (باي) أما بخصوص محيط الدائرة ، فهي عبارة عن طول خط منحني يحد الدائرة ، ولحساب محيطها جبرياً يستعمل القانون التالي : محيط الدائرة = 2 × π × نق أو محيط الدائرة = π × ق.
كيفية إيجاد محيط الدائرة يدوياً:
من المعروف بأن الدائرة تختلف عن الشكل الهندسي ، كون الدائرة خالية من الخطوط المستقيمة ، وهي نتيجة إيصال عدد من النقاط بخط منحن ، ولإيجاد محيط علبة دائرية الشكل باستعمال الخيط ، هنالك عدد من الخطوات التي عليك اتباعها وهي كالتالي:
- أولاً: أحضر خيط أو شريط قياسي طوله مناسب ، بحيث يتم تثبيت طرفه على حافة العلبة باستعمال اللاصق.
- ثانياً : يحاط الطرف الآخر من الخيط حول العلبة الدائرية ، بحيث يكمل دورة كاملة دون نقصان أو زيادة.
- ثالثاً: يحدد مكان الخيط الذي اكتملت الدورة عنده ، ويقص باستعمال المقص.
- رابعاً: يفك الخيط من الناحية التي تم تثبيتها ، ومن ثم يقاس طوله باستخدام إحدى أدوات القياس المناسبة (كالشريق القياسي أو المسطرة) حينها سيكون طول الخيط المقاس مساو لطول الخط المنحني المحيط بالعلبة ، والذي يمثل محيط الدائرة.
للمزيد يمكنك قراءة : علماء الرياضيات العرب والأجانب ونبذة عن ابتكاراتهم
مفاهيم هامة متعلقة بالدائرة:
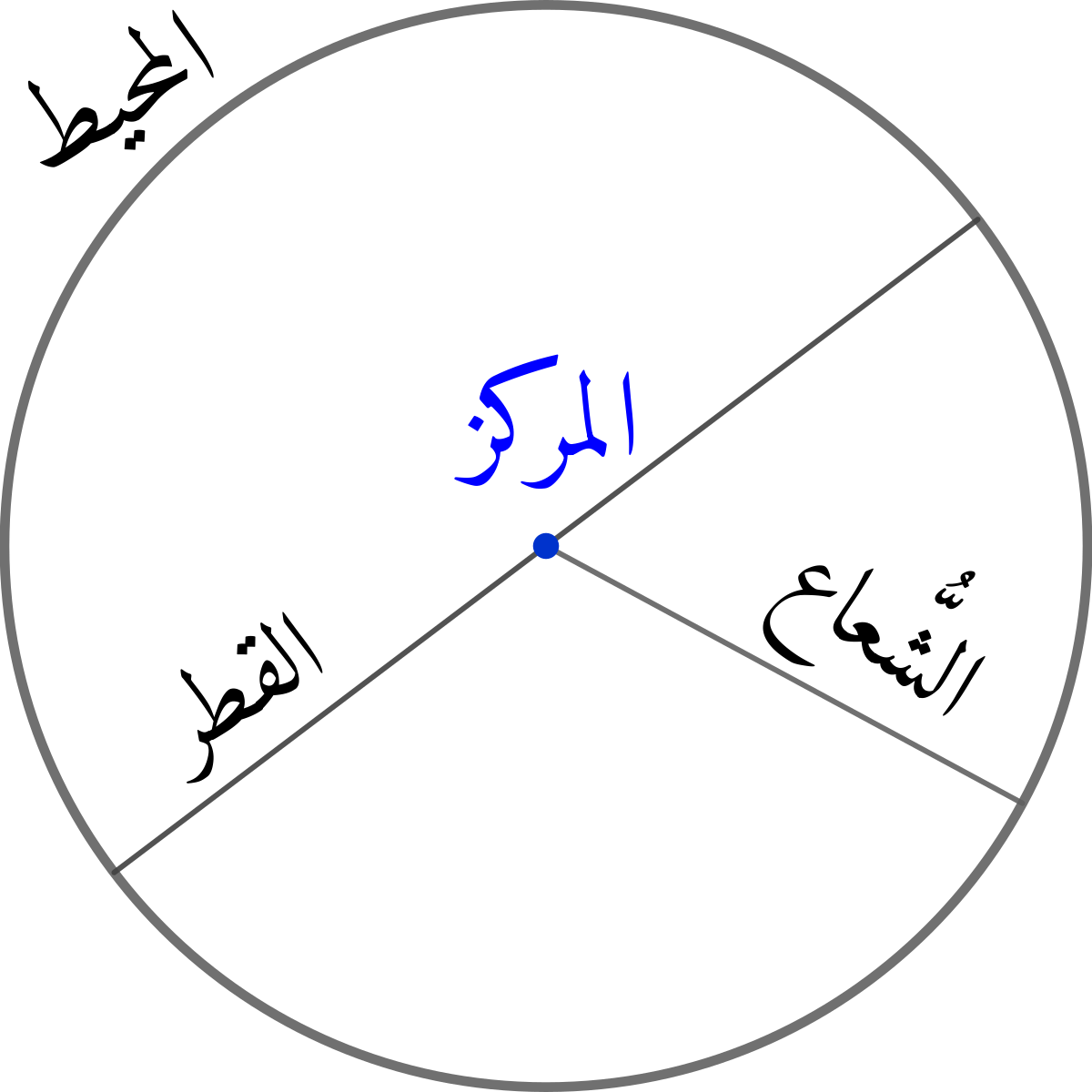
هناك عدد من المفاهيم المعلقة بالشكل الدائري ، ومن تلك المفاهيم:
- مركز الدائرة ويرمز إليه برمز (م) : وهي عبارة عن نقطة واقعة بمنتصف الدائرة ، بحيث تكون المسافة بينها وبين أي نقطة تقع على حواف الدائرة هي مسافة ثابتة.
- قطر الدائرة ويرمز إليه بالرمز (ق) : وهي طول القطعة الواصلة بين نقطتين واقعين على الدائرة ، على شرط أن تمر تلك القطعة بمركز الدائرة.
- نصف قطر الدائرة ويرمز إليه بالرمز (نق) : وهي طول القطعة الواصلة بين المركز وبين أي نقطة واقعة على الدائرة.
- وتر الدائرة : وهي عبارة عن القطعة المستقيمة الواقع جانباها على حدود الدائرة ، وإن حدث أن مرت تلك القطعة بمركز الدائرة ، عندها ستسمى قطراً.
- القاطع : وهو خط مستقيم يقطع الدائرة بنقطتين تقعان على حدود الدائرة.
للمزيد يمكنك قراءة : الغاز في الرياضيات مع الحل
أمثلة توضح كيفية حساب محيط الدائرة:
المثال الأول: عليك حساب محيط غرفة دائرية إن علمت بأن نصف قطرها 7م.
الحل: باستعمال القانون يحسب محيط الغرفة على النحو التالي:
- محيط الدائرة = 2 × π × نق.
- يعوض نق بالقانون وقيمته هو 7م.
- محيط الغرفة = 2 × 22/7 × 7 ، يمكننا أن نبسط المقدار لأبسط صورة كالتالي:
- محيط الغرفة = 2 × 22.
- إذن محيط الغرفة = 44م.
المثال الثاني: عليك حساب محيط دائرة إذا علمت بأن قطرها يساوي 100 ملم.
الحل: باستعمال القانون يتم حساب محيط الغرفة كالتالي:
- محيط الدائرة = π × ق.
- يعوض ق بالقانون وقيمته هو 100م.
- محيط الدائرة = 3.14 × 100.
- إذن محيط الدائرة = 314 ملم.
المثال الثالث : هناك علبة دائرية الشكل طول نصف قطرها هو 0.5 دسم ، أوجد محيطها.
الحل:
- المحيط = 2 × π × نق.
- المحيط = 2 × 3.14 × 0.5.
- المحيط = 3.14 تقريباً.
- إذن محيط أي دائرة طول قطرها واحد يساوي (باي).
للمزيد يمكنك قراءة : بحث عن علم الرياضيات