كيفية حساب الانحراف المعياري والتباين والتشتت من الجدول
محتوي الموضوع
الانحراف المعياري هو درس من دروس مادة الرياضيات يدرسه كلا من طلاب الثانوي وطلاب بعض الكليات العملية بالجامعات لمعرفة كيفية حساب الانحراف المعياري والتباين والتشتت، ويستخدم الانحراف المعياري في قياس مدى تشتت البيانات عن الوسط الحسابي ويرمز له بالرمز سيجما، ويعد الانحراف المعياري هو المقياس الأكثر استخداما من بين مقاييس التشتت لقياس مدى التبعثر الإحصائي، وتكون العلاقة بين تشتت البيانات عن الوسط الحسابي والانحراف المعياري علاقة طردية حيث تزداد قيمة الانحراف المعياري مع ازدياد تشتت البيانات عن الوسط الحسابي ويحدث العكس عندما يقل تشتت البيانات يقل الانحراف المعياري، أما التباين فهو مربع الانحراف المعياري، ويتأثر بالقيم المتباعدة ولا يتأثر بالتغيرات التي تطرأ على العينة، ويتم حساب المتوسط الحسابي عن طريق مجموع القيم أو الاعداد على عددهم، ولتعرف على كيفية الحساب بالتفصيل نقدم لكم عبر موقع احلم موضوع “كيفية حساب الانحراف المعياري” فهيا بنا نتعرف عليه.
كيفية حساب الانحراف المعياري بالتفصيل:
الانحراف المعياري: هو مقياس يستخدم لقياس مدى تجانس البيانات وتناغمها معا أو تباعدها وتفرقها عن متوسطها الحسابي.
مثال: احسب الانحراف المعياري للأرقام الآتية ” 4، 8، 12″.
- أولا نقوم بحساب المتوسط الحسابي لثلاثة أرقام السابقة كالآتي: 4+ 12 ÷2= 8.
- ثم نقوم بحساب الانحراف المعياري لثلاثة أرقام أيضا كالتالي: 4 -8 = -4، 12 -8 = 4 “.
- ثم نقوم بتربيع الناتج: (-4) ^2 =16، (4)^2 = 16 “.
- نقوم بجمع نواتج التربيع كالآتي: “16 + 16 = 32 “.
- ثم نقوم بقسمة الناتج على العدد:” 32 ÷ 2 = 16 “.
- ثم نقوم بإيجاد الجزر التربيعي للناتج السابق: الجزر التربيعي ل16= 4.
- إذا الانحراف المعياري = 4.
مساحة الدائرة تعرف علي القانون وكيفية حساب محيط نصف الدائرة والفرق بين المحيط والمساحة.
مثال على الانحراف المعياري:
احسب الانحراف المعياري لمجموعة القيم الآتية: “5، 6، 8، 10، 4، 3 “.
- أولا نقوم بحساب المتوسط الحسابي = مجموع القيم على عددهم = 5+ 6+ 8+ 10+ 4+3 ÷ 6= 36 ÷ 6= 6 .
- ثم نقوم بإيجاد انحرافات القيم عن وسطها وتربيعها كالآتي : (القيمة – الوسط الحسابي )^2 .
- 6-5=1……….6-6=0…….6-8= -2……6- 10= -4……6-4= 2….6-3= 3 .
- (1)^2=1…..(0)^2=0………(-2)^2=4……(-4)^2=16……(2)^2=4……(3)^2= 9.
- المجموع = 1+0+4+16+4+9=34.
- (ن-1) = 6-1=5 .
- قانون الانحراف المعياري يساوي الجزر التربيعي لمجموع مربعات انحرافات القيم عن المتوسط الحسابي على عددهم ناقص واحد .
- إذا الانحراف المعياري = 34 ÷ 6-1 = 6,8 ، الجزر التربيعي ل6,8 = 2,6.
ارتفاع مثلث متساوي الساقين خصائصه وقانونه وكيفية حسابه.
تعريف التشتت ومقاييسه:
- التشتت: هو أحد خصائص البيانات الذي يتم من خلاله تحديد تجانس القيم مع بعضها البعض وتناغمها أو مدى تبعثر القيم وتباعدها عن بعضها البعض.
- وتشتت البيانات يعني ابتعاد القيم أو البيانات عن بعضها البعض وتبعثرها وعدم تجانسها حول نقطة تركيز معينة، أما تجانس البيانات فيعني تقارب وتجانس القيم او البيانات مع بعضها البعض حول نقطة تركيز معينة.
- مقدار التشتت: يزداد مقدار التشتت كلما بعدت البيانات عن بعضها البعض وتفرقت ، ويقل مقدار التشتت كلما تقاربت البيانات من بعضها البعض .
- ويتم قياس مدى تشتت البيانات أو تجانسها من خلال المقاييس الآتية: “الانحراف المعياري، التباين، نصف المدى الربيعي، المدى، الانحراف المعياري المتوسط “.
مساحة شبه المنحرف تعرف علي كيفية حسابها والقانون الخاص بها وأنواع شبة المنحرف.
التباين وطرق حسابه:
- التباين هو عبارة عن مقياس من مقاييس التشتت التي تعمل على المتوسط الحسابي لمجموع المشاهدات وإيجاد الفرق بين قيمة كل مشاهدة على حدة .
- ويقوم مقياس التباين على أخذ عينة من العينات وإجراء التجارب والأبحاث عليها.
- قانون التباين = مجموع (س – الوسط الحسابي)^2 ÷ (ن-1)
- إذا كان هناك مجموعة من البيانات لعينة في مجتمع ما عددها “س1، س2، س3، س4….س ن.”، فإن الوسط الحسابي يساوي مجموعهم على عددهم.
- قانون التباين في البيانات المبوبة = مجموع ( س – الوسط الحسابي )^2 × (تكرار الفئة ) ÷ (ن-1) .
مثال:
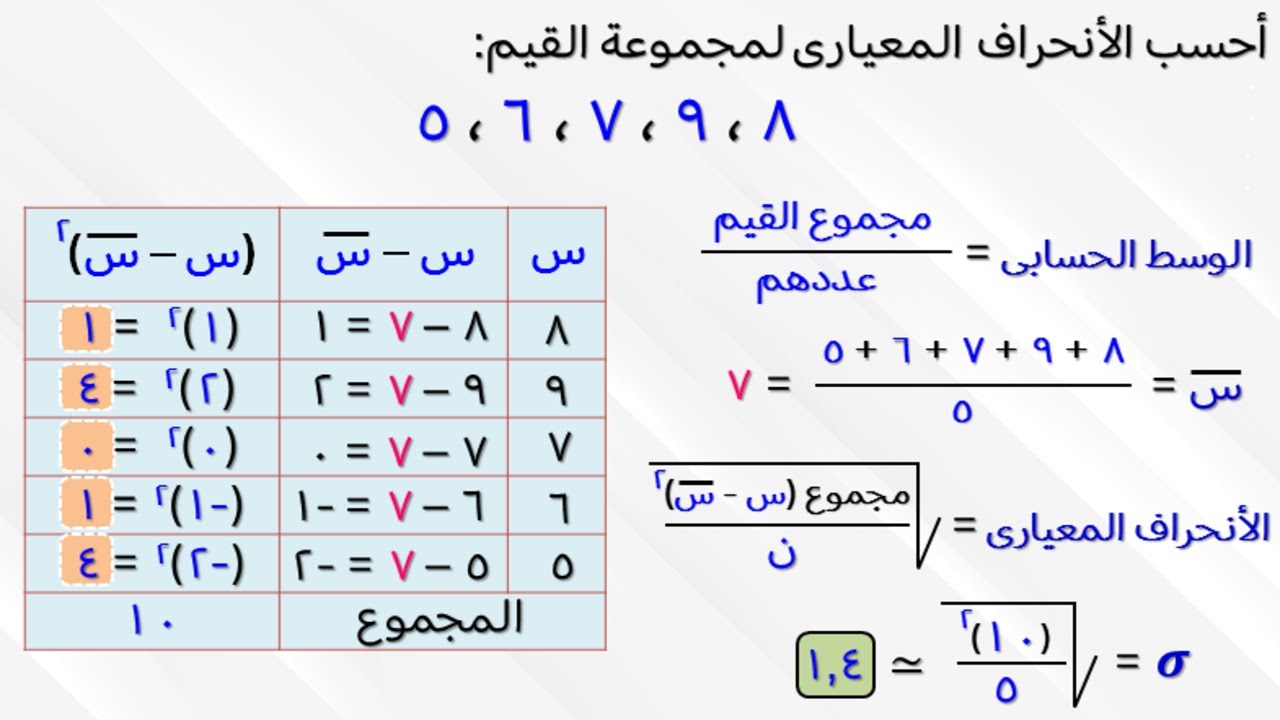
في أحد أقسام كلية الهندسة تم اختبار الطلاب في مادة التصميم وكانت نتائج الاختبار لعينة من الطلاب كالاتي: “5 ، 6، 7، 8، 9 من 20 العلامة النهائية”، المطلوب احسب التباين لعينة الطلاب؟
- أولا نقوم بحساب الوسط الحسابي كالآتي: الوسط الحسابي = “5+6+7+8+9” ÷ 5 = 35 ÷ 5= 7 .
- ثم نجد قيمة (ن -1 ) = 5-1=4 . وهو عدد النتائج ناقص واحد.
- ثم نقوم بحساب الانحراف من القيم السابقة “5،6، 7، 8، 9 “.
- الانحراف = س – الوسط الحسابي = 5-7 = -2 …… 6 – 7 = -1 ….. 7-7 = 0 …… 8-7 = 1 …… 9- 7 = 2 .
- مربع الانحراف = (س – الوسط الحسابي )^ 2 = (-2)^2 = 4 ….(-1)^2 = 1……(0)^2 = 0……(1)^2 = 1……(2)^2= 4 .
- مجموع قيم مربع الانحراف = 4+ 1+ 0+ 1+ 4 = 10.
- التباين = المجموع (س – الوسط الحسابي)^2 ÷ (ن-1) = 10 ÷ 4= 2.5 .
مثال على حساب التباين في البيانات المبوبة:
إذا كانت عينة درجات الطلاب في أحد الكليات كالاتي: “2،4، 6، 7، 8، 9″، وكان تكرار 2 إلى فئة “0-5” إذا فما هو التباين للتوزيع التكراري؟
- أولا نقوم بإيجاد المتوسط الحسابي الذي يساوي مجموع الدرجات على عددهم = 36 ÷6 =6 .
- ثم نقوم بحساب تكرار الفئة كالاتي: تكرار الفئة من (0-5) = (0+ 5 ) ÷ 2 = 2,5 .
- نقوم باستخدام تكرار الفئة إثنين ونصف لكل الفئات بالجدول.
- ثم نقوم بإيجاد قيمة (ن-1) = (6-1) =5 .
- ثم نقوم بحساب مربعات انحرافات القيم عن طريق طرح قيمة الوسط الحسابي من كل قيمة لدرجات الطلاب ثم تربيع الناتج = (س- الوسط الحسابي) ^2
- مثال : 6 – 4=2….6-2=4…….6-6=0…….6-7=-1….6-8=-2….6-9=-3، ثم نربع القيم كالاتي: (2)^2=4….(4)^2=16…(0) ^2=0…..(-1)^2=1….(-2)^2=4…..(-3)^2=9 .
- ثم نقوم بجمع قيم الانحرافات السابقة =4 +16 + 0+ 1+ 4+ 9= 34.
- قانون التباين يساوي مربع الانحراف في تكرار الفئة على عدد قيم الدرجات ناقص واحد.
- التباين = مجموع(س- الوسط الحسابي )^2 × تكرار الفئة ÷ (ن -1)= 34 × 2,5 ÷ 6-1 = 85 ÷ 5 = 17.
ارقام وكلمات 
قانون الإنحراف 
قوانين التباين
اهمية الحاسوب في التعليم وأثاره الإيجابية والسلبية على المجتمع.
إلى هنا نكون قد وصلنا غلى ختام موضوع “كيفية حساب الانحراف المعياري والتباين والتشتت من الجدول” الذي عرفنا من خلاله أن الإنحراف المعياري والتباين هما إحدى مقاييس التشتت وأن الإنحراف المعياري أدق المقاييس للتشتت الذي يحدد مدى تجانس بيانات العينات وتقاربها حول نقطة معينة أو تبعثرها وتفرقها عن بعضها البعض، كما عرفنا من خلال الموضوع أن الوسط الحسابي لمجموعة قيم هو جمعهم على عددهم، كما ذكرنا أمثلة متنوعة على التباين والإنحراف المعياري توضح لطلاب طريقة حساب التباين والإنحراف المعياري.
وأخيرا نتمنى ان تكونوا استفدتوا من قراءة الموضوع ……مع تمنياتنا بالتوفيق لكل الطلاب في مراحلهم التعليمية…….