محتوي الموضوع
بإمكاننا أن نعرف المستطيل على أنه شكل رباعي الأضلاع لديه أربع زوايا قائمة ، ويعد حالة خاصة من متوازي الأضلاع ، بحيث تكون الأضلاع المتقابلة متوازية ومتساوية في الطول ، ولدى المستطيل اثنان من الأضلاع المتقابلة ، ومن الممكن أن يختلف كل زوج عن الآخر بالنسبة للطول ، إلا أن أضلاع الزوج الواحد متساوية في الطول ، أما بالنسبة لأقطار المستطيل فتكون متساوية في الطول وتنصف بعضها البعض وذلك عند نقطة التقاطع ، وتقسم المستطيل لمثلثين متطابقين ، فتشكل زوايا متنوعة ، إحداها منفرجة والأخرى حادة ، ولو كانت الزوايا التي تتشكل بين القطرين هي زوايا قائمة فالشكل هو مربع ، ومن الجدير بالذكر أن كل قطر للمستطيل يشكل قطراً للدائرة التي تحيط به تماماً ، وفي هذا اليوم سوف نتعرف أكثر حول قانون المستطيل فتابعوا معنا:
حالات خاصة من المستطيل:
- المربع: والمربع هذا عبارة عن مستطيل إلا أن جميع أضلاعه تتساوى في الطول.
- مستطيل فيبوناتشي: ونسبة طول هذا المستطيل إلى عرضه هي 1.618 ، بمعنى أن طوله أكبر من عرضه بـ1.618 مرة ، فعلى سبيل المثال : لو كان المستطيل 2 فسوف يكون العرض : 1.618 × 2 = 3.236 ، ويطلق على هذا المستطيل أيضاً اسم المستطيل الذهبي لأن نسبته هي النسبة الذهبية 1.618.
قوانين حساب محيط المستطيل:
بإمكاننا أن نعرف محيط المستطيل على أنه المسافة الإجمالية حول سطح المستطيل ، ويتم قياس المحيط باستعمال إحدى وحدات قياس الطول ، وهناك عدة طرق يتم من خلالها حساب محيط المستطيل ، ومنها:
حساب المحيط باستعمال الطول والعرض:
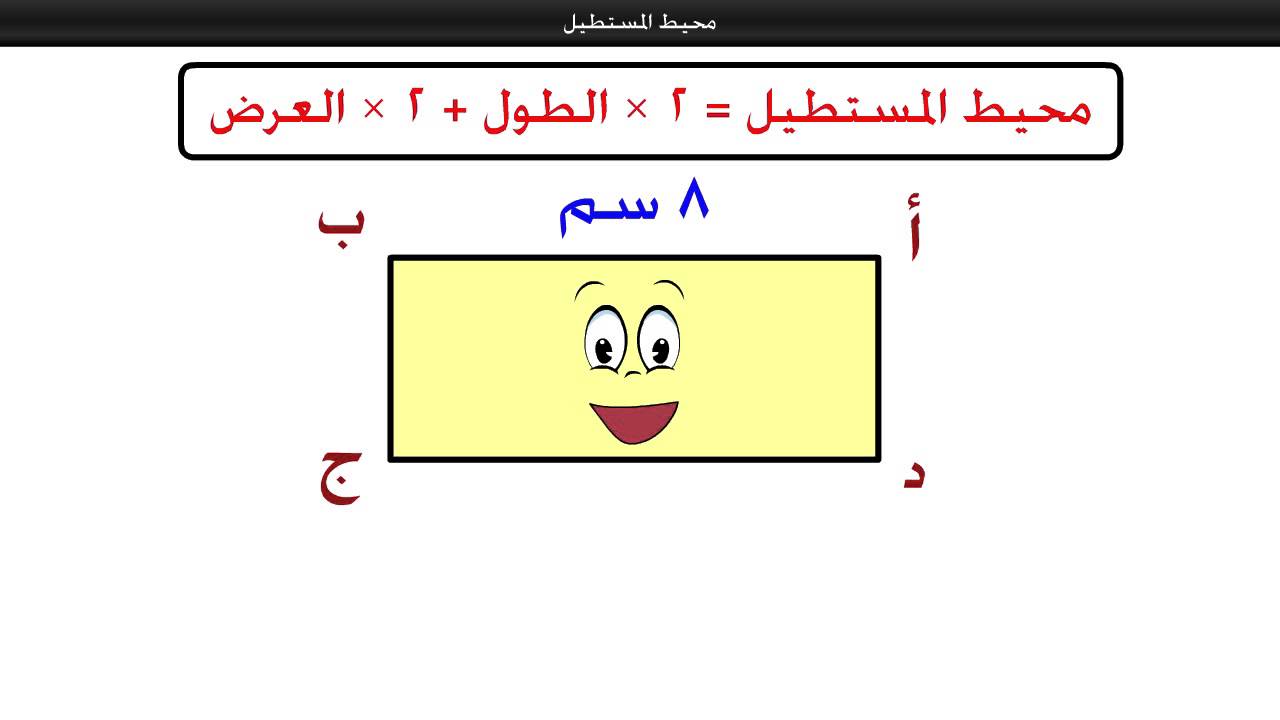
وهذا القانون يعد الأكثر شيوعاً ، وهو يساوي ضعفي مجموع الطوال والعرض ، حيث:
محيط المستطيل = 2 × (الطول + العرض) وبالرموز : ح = 2 (أ + ب) حيث:
أ : طول المستطيل.
ب : عرض المستطيل.
حساب المحيط باستعمال العرض أو القطر والطول ، حيث:
محيط المستطيل = 2 × الطول + 2 (القطر2 – الطول2) ، وبالرموز : ح = 2أ + 2 (ق2 – أ2) ، أو محيط المستطيل = 2 × العرض + 2 (القطر2 – العرض2) ، وبالرموز : ح = 2ب + 2 (ق2 – ب2) : حيث:
أ : طول المستطيل.
ب : عرض المستطيل.
ح : محيط المستطيل.
ق : قطر المستطيل.
حساب المحيط باستعمال العرض أو المساحة والطول ، حيث:
محيط المستطيل = 2 × الطول + 2 × (المساحة / الطول) ، وبالرموز : ح = 2أ + 2 (م / أ) ، أو محيط المستطيل = 2 × العرض + 2 × (المساحة / العرض). ، وبالرموز : ح = 2ب + 2 (م/ب) حيث :
أ : طول المستطيل.
ب: عرض المستطيل.
م : مساحة المستطيل.
للمزيد يمكنك قراءة : محيط المستطيل
قوانين حساب مساحة المستطيل:
بإمكاننا أن نعرف مساحة المستطيل على أنها مقدار الفراغ أو الحيز المحصور بداخل المستطيل ، ويتم القياس من خلال وحدة الطول المربعة ، ويتم حسابها بالعديد من الطرق وهي كالآتي:
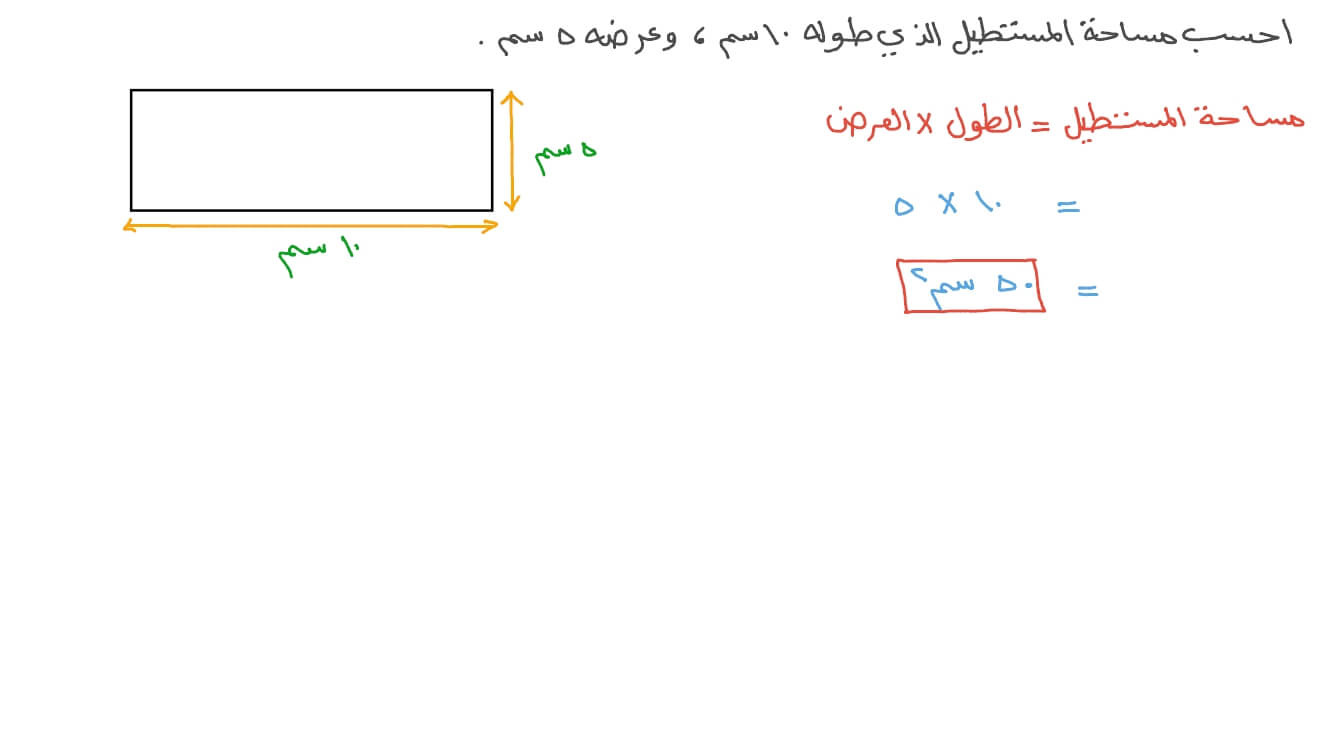
باستعمال الطول والعرض : وهذا القانون يعد الأكثر شيوعاً ، ويساوي طول المستطيل مضروباً في عرضه ، حيث:
مساحة المستطيل = الطول × العرض ، وبالرموز : م = أ × ب ، حيث :
أ : طول المستطيل.
ب : عرض المستطيل.
حساب المساحة باستعمال المحيط والطول أو العرض ، حيث :
مساحة المستطيل = محيط المستطيل × الطول – 2 × الطول2) / 2 ، وبالرموز : م = (ح أ – 2 أ2) /2 ، أو مساحة المستطيل = محيط المستطيل × العرض – 2× العرض2) /2 ، وبالرموز = م = (ح ب -2 ب2) /2 ، حيث :
أ : طول المستطيل.
ب : عرض المستطيل.
ح : محيط المستطيل.
م : مساحة المستطيل.
حساب المساحة باستعمال القطر والطول أو العرض ، حيث:
مساحة المستطيل = الطول × (القطر2 – الطول2) ، وبالرموز : م = (ق2 – أ2) ، أو مساحة المستطيل = العرض × (القطر2 – العرض2) ، وبالرموز : م = ب (ق2 – ب2) ، حيث :
أ : طول المستطيل.
ب : عرض المستطيل.
ق : قطر المستطيل.
م : مساحة المستطيل.
للمزيد يمكنك قراءة : اهداف تدريس الرياضيات
قوانين حساب أقطار المستطيل:
بإمكاننا أن نحسب أطوال أقطار المستطيل بطرق كثيرة ، ومنها:
باستعمال نظرية فيثاغورس : وفيها نأخذ الجذر التربيعي لمجموع مربعي العرض والطول ، لينتج الآتي:
قطر المستطيل = (الطول2 + العرض2) ، وبالرموز : ق = (أ2 + ب2) : حيث :
ق : قطر المستطيل.
أ : طول المستطيل.
ب : عرض المستطيل.
حساب القطر باستعمال المساحة والعرض أو الطول ، حيث :
قطر المستطيل = (المساحة2 / الطول2 + الطول2) ، وبالرموز : ق = (م2 / أ2 / أ2) ، أو قطر المستطيل = (المساحة2 / العرض2 / العرض2) ، وبالرموز : ق = (م2 / ب2 + ب2) ، حيث:
ق : قطر المستطيل.
أ : طول المستطيل.
ب : عرض المستطيل.
م : مساحة المستطيل.
للمزيد يمكنك قراءة : محيط المربع
مسائل مصورة: