محيط المثلث تعرف علي قانونه وكيفية حسابه وانواع المثلثات

المثلث هو واحد من الاشكال الهندسية الاساسية له ثلاثة ابعاد، وقد عرف رسم المثلث منذ اقدم العصور كما تم استخدامه في الكثير من الحضارات والديانات للدلالة علي القدسية، مثل الديانة المسيحية التي اتخذت من الثالثو اي الثلاثي رمزاً لمعتقدها الديني، بالاضافة الي الحضارة الفرعونية القديمة التي اتحذت الاهرمات علي شكل موشورات مثلثة الوجوع للاشارة الي الجبروت والعظمة وغيرها العديد من الحضارات في مختلف انحاء العالم، والمثلث له ثلاثة اضلاع وثلاثة رؤوس وثلاثة زوايا داخلية وثلاثة اقطار تتلاقي جميعاً في منتصف المثلث، كما يتميز المثلث بوجد زوايا خارجية له ايضاً ومحيط المثلث هو قياس المسافة حول الشكل ثنائي الابعاد اي انه حاصل جمع اطوال اضلاع الشكل الثلاثة، ولإيجاد محيط المثلث نقوم بحساب جمع اطوال اضلاعة الثلاثة وسيكون الناتج وقتها ذا بعد واحد ويسعدنا ان نستعرض معكم الآن في هذا المقال عبر موقع احلم معلومات رياضية مفيدة وهامة حول المثلث وانواع وكيفية حساب محيط المثلث والمعادلة الخاصة به وللمزيد يمكنكم زيارة قسم : تعليم .

انواع المثلث

حسب قياس الزوايا

• مثلث قائم الزاوية له زاوية واحدة قائمة قياسها 90°.
• مثلث منفرج الزاوية واحدة من زواياه الثلاث قياسها أكبر من 90°.
• مثلث حاد الزاوية قياس جميع زواياه أقل من 90°.

حسب طول الاضلاع

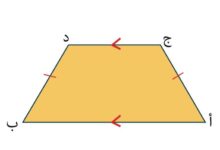
• مثلث متساوي الاضلاع وبالتالي فإن قياس زواياه متطابقة وتساوي 60°.
• مثلث متساوي الساقين ويكون طول الضعلين القامين علي القاعدة متساويين وبالتالي فإن قياس الزاويتين على القاعدة متطابقتين في الوقت نفسه.
• مثلث مختلف الأضلاع .

قانون محيط المثلث

محيط المثلث يساوي مجموع اطوال اضلاعة، بمعني اننا نجمع طول الضلع الاول و الضلع الثاني والثالث للحصول علي مقدار محيطة، ولكن لابد من مراعاة وحدة طول الاضلاع، فيجب ان تكون جميعها بالسم او بالملي او بالمتر وهكذا، ويمكن التعبير عن قانون محيط المثلث بصيغة رياضية كما يأتي: محيط المثلث=أ+ب+ج، حيث إنَّ أ، ب، ج طول أضلاع المثلث.

قانون فيثاغورس

اكتشف العالم فيثاغورس قبل 2000 سنة من الآن قانون يخص المثلث القائم الزاوية، وهذا القانون ينص علي انه يمكن ايجاد مربع وتر المثلث وهو اطول ضلع في المثلث القائم الزاوية من خلال جمع مُربّع كُل ضلع من الضّلعين الآخَرَين، ويتمّ التّعبير عن هذا القانون عن طريق المعادلة التالية : الوتر2 = الضلع الأوّل2 + الضلع الثاني2، ويمكن بعد ذلك الحصول على طول الضلع عن طريق إيجاد جذر الناتج .