محتوي الموضوع
من الممكن لنا أن نعرف النسبة المئوية على أنها النسبة التي يشكل العدد 100 الجزء الثاني منها ، وترجع كلمة النسبة المئوية في الأصل للكلمة اللاتينية Per Centum ومعناها (لكل مئة) ، وفي العادة يتم التعبير عنها في الرياضة بالرمز % ، ومن الممكن التعبير عنها أيضاً بأشكال أخرى بعد أن تحول لكسور عادية أو عشرية ، فمثلاً من الممكن كتابة النصف على صورة النسبة المئوية 50% ، أو العدد العشري 0.5 ، أو الكسر العادي 2/1 ، ومن ضمن الأمثلة الأخرى على النسب المئوية 100%=100/100=1، 40%=40/100=4/10=2/5=0.4.
مفهوم النسبة المئوية:
- يمكننا أن نوضح مفهوم النسبة المئوية بصورة أكثر بساطة عن طريق تخيل تقسيم بيتزا كبيرة على سبيل المثال إلى 100 جزء صغير ، ففي تلك الحالة كل جزء من تلك الأجزاء يشكل نسبة 1% من البيتزا ، أما ربع البيتزا فيشكل ما نسبته 25% منها ، والبيتزا كاملة يتم التعبير عنها بنسبة 100% ، ومن ضمن الأمثلة الواقعية أيضاً هو التعبير عن عدد الأيام الماطرة من مجموع الأيام الكلي أثناء فترة محددة من الفترات على شكل نسبة مئوية.
- فعلى سبيل المثال لو كان الجو ماطر لمدة امتدت إلى 14 يوم أثناء مدة 100 يوم فائتة ، فإنه من الممكن التعبير عن ذلك الأمر كنسبة مئوية على شكل 100 / 14 = 14 ، وذلك يعني أن أربعة عشر يوم كان ماطر من أصل مائة يوم خلال المدة السابقة ، كما أن قول محتويات تلك الصندوق مكونة بنسبة 75% من التفاح فذلك الأمر يعني أن التفاح يكون خمسة وسبعون غرض من كل مائة غرض من محتوياته.
للمزيد يمكنك قراءة : اهداف تدريس الرياضيات
حساب النسبة المئوية:
يتم تعريف النسبة المئوية على أنها عملية إسناد أي رقم لمئة ، ومن الممكن تحويل أي رقم لنسبة مئوية وذلك عن طريق إتباع ما يلي حسب حالته:
- حساب النسبة المئوية لنظام معين : إن النسبة المئوية تعد طريقة من الممكن بواسطتها التعبير عن أحد الأعداد كجزء أو حصة من سلسلة من الأعداد ، ومن الممكن حسابها باستعمال الصيغة العامة أو باستعمال القانون التالي : النسبة المئوية = [القيمة / القيمة الكلية] × 100% ، أو النسبة المئوية = [الجزء / الكل) × 100% ، وبناءً عليه من الممكن حساب النسبة المئوية لنظام ما عن طريق تقسيم عدد الأشخاص أو الحاجيات التي يراد معرفة نسبتها على العدد الكلي للمجتمع أو الحاجات المشمولة في تلك الدراسة ، وبعدها يتم ضرب الناتج النهائي بالعدد مائة ، فعلى سبيل المثال من الممكن حساب نسبة الأشخاص المالكين لبطاقة اشتراك مكتبية لو كان عددهم ثمانية وثلاثون فرد ضمن مجتمع معين يبلغ عدد أفراده مائتين وثلاثون ، من خلال تعويض الأعداد بالمعادلة السابقة ، لينتج أنه 230 / 38 × 100% = 16.5% ، وهذا الأمر يعني أن 16.5 شخص من كل مائة شخص من الأشخاص في هذا المجتمع لديهم بطاقة مكتبية ، أو أن نسبة 16.5% من هذا المجتمع لديهم بطاقة مكتبية.
- تحويل الكسر العادي لنسبة مئوية : إن أي كسر عادي مكون من بسط ومقام ، إذ أن البسط يتمثل بالعدد الموجود بالأعلى ، أما بخصوص المقام فهو العدد الذي يوجد بالأسفل ، وعندما نقوم بتحويل الكسر لنسبة مئوية فإن هذا يعني جعل المقام مساوي للعدد مائة ، ولتحقيق هذا فإننا بحاجة لضرب العدد الذي يوجد بالمقام برقم آخر مناسب لجعله مساوي للعدد مائة ، وضرب البسط أيضاً بنفس ذلك العدد ، وذلك من أجل الحفاظ على قيمة الكسر من غير تغيير ، فمثلاً من الممكن تحويل الكسر 25 / 4 لنسبة مئوية من خلال ضرب كل من البسط والمقال بالعدد أربعة ، كي ينتج أن 25 / 4 = 100 / 16 = 16% ، وبالمقابل من الممكن تحويل النسبة المئوية ببساطة لكسر عادي من خلال وضع قيمة النسبة المئوية على مقام قيمته العدد مائة ، وبعدها يتم تبسيط الكسر لأبسط صورة ممكنة ، فعلى سبيل المثال تحويل النسبة 50% بحاجة لكسر عادي ، كتابة العدد 50% على هيئة 100 / 50 ، وبعدها يتم تبسيط الكسر كما يلي : 50/100=5/10=1/2.
العمليات الحسابية على النسب المئوية:
إن من أبسط العمليات الحسابية على النسب المئوية ما يلي :
- ضرب وقسمة النسب المئوية : إن ضرب النسب المئوية أو قسمتها بحاجة لكتابتها أولاً على صورة أعداد عشرية أو كسور عادية ، فعلى سبيل المثال ضرب النسبة الآتية 10% ، 20% ، 30% ببعضها بحاجة لتحويلها أولاً لكسور عادية ، وبعدها تضرب كالمعتاد ، كما يلي : 10/100×20/100×30/100=6/1000=0.6%
للمزيد يمكنك قراءة : بحث عن مادة الرياضيات
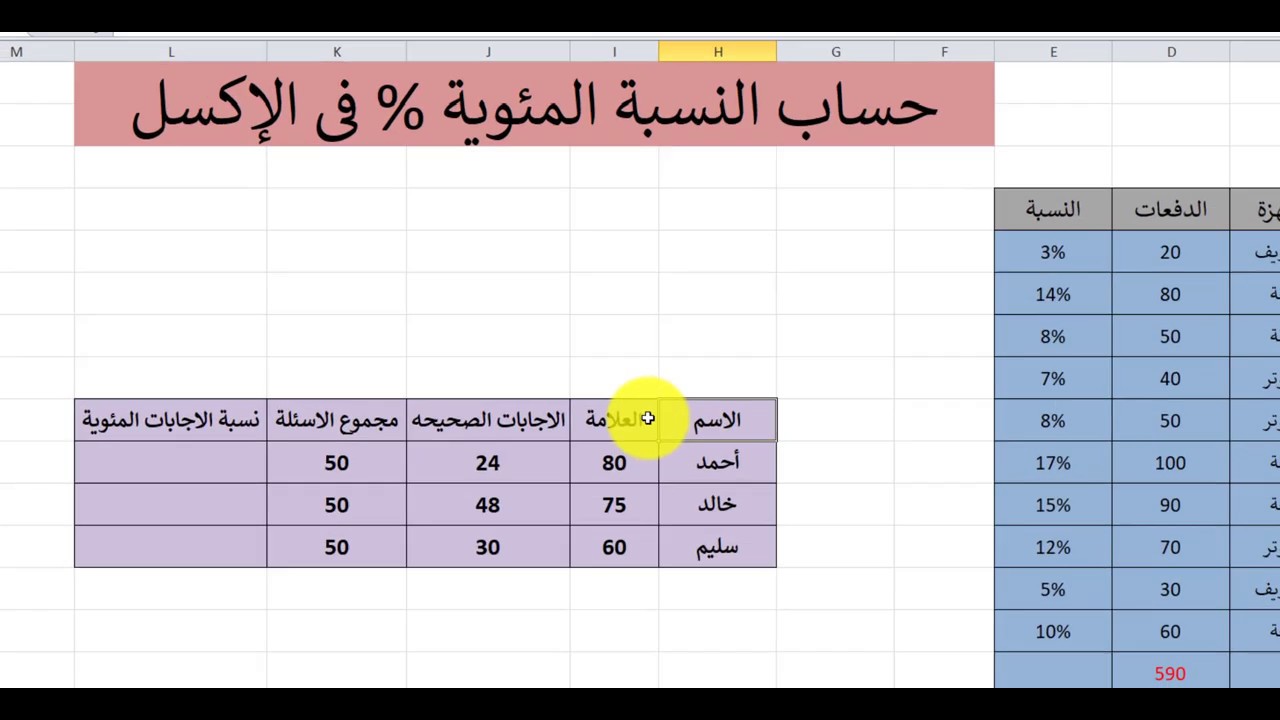
عمليات حسابية مصورة:
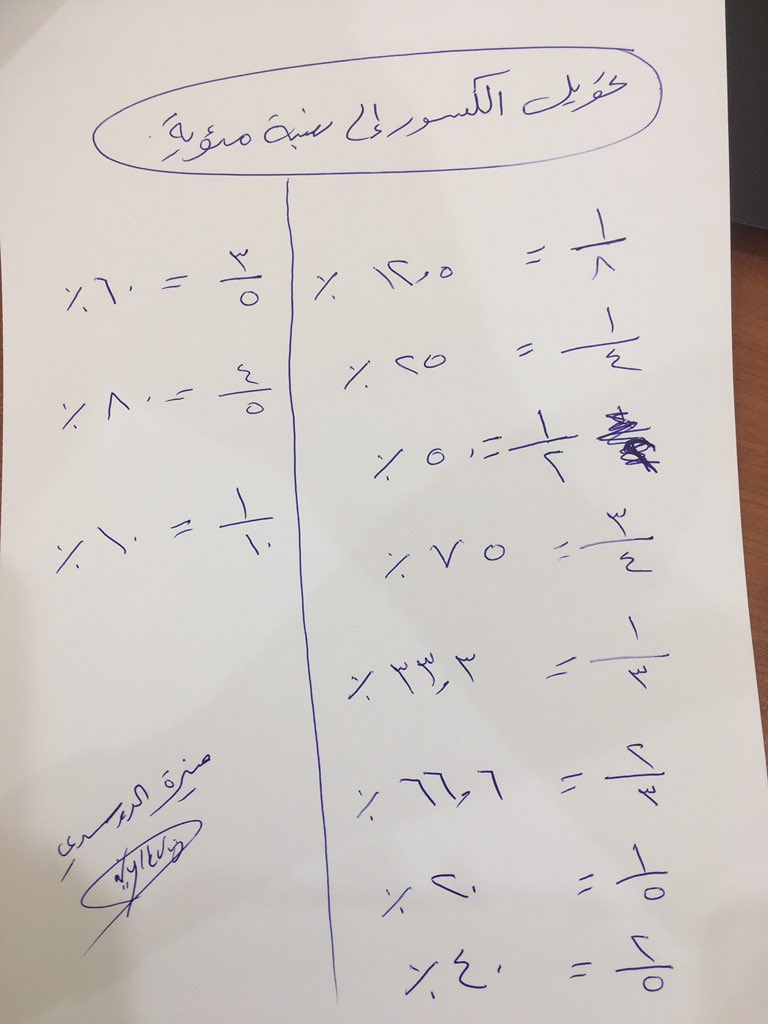

للمزيد يمكنك قراءة : الغاز رياضيات