خط تماثل ومحوره في الرياضيات للصف الرابع
محتوي الموضوع
خط تماثل ومحوره في الرياضيات للصف الرابع ؛ في البداية لا بد من الإشارة إلى أن علم الرياضيات قائم على دراسة البنية ، والأنماط والفراغ بالإضافة لمعدلات التغير ، إذ أن الرياضيات تقوم بالتعامل مع كلاً من : منطق الأشكال ، والكميات ، بالإضافة للترتيب ، ويسعى عباقرة الرياضيات وعلمائها لصياغة فرضيات أخرى جديدة بغرض تأسيس الحقائق ، وهذا من خلال الاستنتاجات الدقيقة من الكثير من البديهيات والتعاريف المختارة بصورة ملائمة.
ونشير هنا لأن علم الرياضيات يمثل اللبنة الرئيسية لكل شيء ، حيث يتواجد في كل شيء في حياتنا اليومية ، بما في هذا الهندسة المعمارية والنقود والفن والرياضة وغيرها ، وتعتبر الرياضيات بالنسبة لعلمائها عبارة عن أداة تحليلية يتم تطبيقها على البيانات التجريبية بغرض إنشاء صيغة تقوم بوصف بعض الاتجاهات الرئيسية للطبيعة ، كما يتم استعمالها مع النظريات التي توجد في الوقت الحالي بغرض استنتاج كميات غير معروفة ، وفي هذا اليوم سوف نتعرف على خط تماثل ومحوره في الرياضيات للصف الرابع ، فقط تفضلوا بالمتابعة معنا.
فروع علم الرياضيات:
نستطيع أن نصنف علم الرياضيات بشكل على لعدة فروع ، سوف نأتي على تفصيل كل فرع منهم في التالي :
- الجبر : وهو عبارة عن نوع من العمليات الحسابية ، حيث يستعمل من أجل حساب كميات ليست معلومة مع الأعداد ، إذ يتم التعبير عن الكميات غير المعروفة من خلال أحرف أبجدية ، ويساهم استعمال الأرقام على تعميم هذه الصيغ والقواعد بهدف إيجاد القيمة المجهولة بالتعبيرات والمعادلات الجبرية.
- الحساب : ويعتبر هذا الفروع واحداً من أقدم فروع الرياضيات وأساسها ؛ وفيه يتم التعامل مع الأعداد والعمليات الرئيسية ، على سبيل المثال : الجمع والضرب والطرح.
- الهندسة : تعتبر واحدة من أكثر فروع علم الرياضيات عملية ، إذ تهتم بالأشكال والأحجام وخصائصها ، وتمثل النقاط والخطوط بالإضافة للزوايا والأسطح والمجسمات العناصر الرئيسية لفرع الهندسة.
- التحليل : وهذا العلم مختص بدراسة معدل التغيير بكميات متفاوتة ، ولا بد من الإشارة لأن التفاضل والتكامل يعدان أساس التحليل.
- علم المثلثات : وهذا علم مشتق من مصطلحين يونانيين ألا وهما : المثلث ، أما المصطلح الثاني فيشير للقياس ، وعلم المثلثات مختص بدراسة العلاقات ما بين زوايا وأضلاع المثلثات.
نظرة عامة حول خط التماثل:
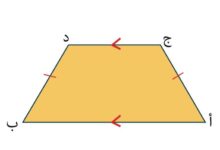
نستطيع أن نعرف خط التماثل على أنه الخط الذي يقوم بفصل الصورة الهندسية لنصفين متساويين تماماً ، بمعنى بحال محاولة ثني الصورة الهندسية عند هذا الخط فإن الجزأين سوف يتوافقين تماماً.
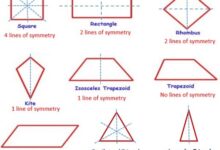
ويختلف عدد خطوط التماثل من صورة هندسية لأخرى ، فعلى سبيل المثال إن للمربع 4 خطوط تماثل ؛ أما بخصوص الدائرة فتمتلك عدد غير نهائي من خطوط التماثل ، أما بخصوص متوازي الأضلاع فليس هناك أي خطوط تماثل به.
- إن عدد خطوط التماثل للدائرة هو لا نهائي.
- وعدد خطوط التماثل للمربع هو 4 خطوط.
- وعدد خطوط التماثل للشكل السباعي يبلغ 7 خطوط تماثل.
- بينما عدد خطوط التماثل لشكل المعين هو خطان تماثل.
- وعدد خطوط التماثل لشكل الطائرة الورقية يبلغ خط واحد فقط.
- بينما يبلغ عدد خطوط التماثل للشكل السداسي 6 خطوط تماثل.
للمزيد يمكنك قراءة : في اي مما يلي يكون الخط المنقط خط تماثل
عدد خطوط التماثل للمثلث:
- بخصوص المثلث الذي يعد صورة هندسية لديها 3 زوايا و3 ضلوع ، فإن عدد خطوط التماثل فيه يختلف من نوع لنوع آخر.
- فعلى سبيل المثال : المثلث الذي يكون متساوي الأضلاع يمتلك 3 خطوط تماثل ، ويعتبر المثلث الذي تتساوي فيه قياسات كافة الزوايا ويكون قياس كل زواية ستون درجة ، وقياسات كافة الأضلاع.
- أما بخصوص المثلث مختلف الأضلاع وهو عبارة عن المثلث الذي لا يتساوي فيه قياس أي ضلع أو أي زاوية فليس هناك خطوط تماثل نهائياً.
- أما بخصوص النوع الأخير من أنواع المثلثات ألا وهو : المثلث متساوي الساقين ، وهو عبارة عن مثلث يتساوي فيه قياس زاويتين وقياس ضلعين ، فيمتلك خط تماثل وحيد.
- ومن أجل وجود خط تماثل للمثلث لا بد على ذلك الخط أن يعبر رأساً واحداً للمثلث وذلك على أقل تقدير ، بالإضافة لأن يفصل ما بين ضلعين متساويين بالطول عن بعضهما البعض.
- ألا وهما : الضلعان اللذان يمران برأس المثلث المحدد ، فعلى سبيل المثال : لو كانت قياسات أطوال أضلاع المثلث هي أ = 4 سنتيمتر، ب = 4 سنتيمتر، جـ = 3 سنتيمتر.
- فلا بد وأن يكون خط التماثل لذلك المثلث فاصل ما بين الضلعين أ = 4 سنتيمتر، ب = 4 سنتيمتر ، وأن يقوم بالمرور من زاوية أو رأس التقائهما سوياً.
- أما بخصوص المثلث الذي تبلغ قياسات أضلاعه فيه على سبيل المثال اثنين سنتيمتر ، أربعة سنتيمتر ، خمسة سنتيمتر ، فليس هناك خطوط تماثل فيه ، وذلك لعدم تواجد ضلعين متطابقين في الطول فيه.
للمزيد يمكنك قراءة : محيط المربع وخصائصه والقانون الخاص به
محور التماثل في الرياضيات:
- محور التماثل يتم تعريفه على أنه الخط المستقيم الذي يقوم بتقسيم الرسم البياني للدالة الى قسمين متساويين, ويحسب عن طريق المعادلة التالية س= -ب/2*أ إذ ان ب هو معامل س و أ هو معامل س^2 في المعادلة ص= س^2+ ب*س+ج, ومثلاً في المعادلة ص=-2س^2+4س-3 يكون س= -4/-2*2=1 اي ان معادلة محور التماثل هي س= 1.
- ويعني ان محور التماثل متطابق لمحور الصادات ويقطع محور السينات عند النقطة (1,-1) ، وإلى هنا متابعينا الكرام متابعي موقع احلم نكون قد وصلنا إلى ختام مقال الليلة وقد تكلمنا فيه ودار حديثنا حول خط تماثل ومحوره في الرياضيات للصف الرابع.
للمزيد يمكنك قراءة : الاشكال الرباعية أنواعها وخصائصها العامة وخصائص كل شكل