الشكل الرباعي الذي فيه ضلعان فقط متوازيان هو ؟
محتوي الموضوع
“الشكل الرباعي الذي فيه ضلعان فقط متوازيان هو ؟” .. في عالم الهندسة الهائل والمعقد، هناك ألغاز تثير فضول العقول وتجذب انتباه المفكرين. واحدة من هذه الألغاز هي الشكل الرباعي الذي يحتوي على ضلعين فقط متوازيين. هل تساءلت يومًا عن هذا الشكل وما إذا كان حقًا ممكنًا؟ إنه سؤال يثير الفضول ويطلق التحدي لأفهم هذا الظاهرة الهندسية المميزة.
قد يبدو الأمر بسيطًا – ضلعين متوازيين – ولكن هذا السؤال يثير العديد من الأسئلة حول الخصائص الهندسية والتصاميم الممكنة. هل هناك شكل محدد يمكن أن يحتوي على هذه الخصائص؟ هل يمكن أن يكون هذا الشكل ذو أهمية في الحياة اليومية أو في العلوم والتكنولوجيا؟
سيكون هذا المقال رحلة استكشافية لاكتشاف الإجابات على هذا السؤال الغامض. سنقوم بدراسة الأشكال الهندسية وتحليل الخصائص التي تجعل شكلًا معينًا يمكن أن يحتوي على ضلعين متوازيين. سنبحث عن الأمثلة ونفهم كيفية تطبيق هذه الفكرة في العمليات اليومية وفي ميادين مختلفة من العلوم.
ما معنى متوازيان
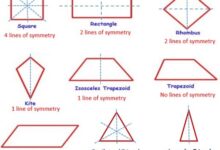
كلمة “متوازيين” تُشير إلى وضعية حيث هناك خطان أو قطعتان مستقيمتان تواجهان بعضهما البعض في الفضاء الثلاثي الأبعاد، وبغض النظر عن امتدادهما، يظلوا متوازيين دون أن يلتقوا. المسافة بين هذين الخطين تبقى ثابتة على طول خط التوازي، وعند مقاطعتهما بخطين آخرين، يكوِّنوا شكلًا رباعيًا يتألف من أربعة أضلاع وأربع زوايا. أمثلة على هذا الوضع تشمل المربع والمستطيل، بالإضافة إلى شبه المنحرف الذي يتكون من ضلعين متوازيين ومتساويين في الطول فقط.
باختصار، “متوازيان” يشير إلى تواجد خطين أو قطعتين مستقيمتين يمكن أن تمتد بلا اتصال بينهما وبشكل متوازي، وهذا يُظهر في تكوين الأشكال الهندسية ذات الأضلاع المتوازية.
الشكل الرباعي الذي فيه ضلعان فقط متوازيان هو
الشكل الرباعي الذي فيه ضلعان فقط متوازيان هو “شبه المنحرف”. يتميز هذا الشكل بوجود ضلعين مستقيمين يعتبران متوازيين، ويميزه عدم تواجد ضلعين آخرين متوازيين أو مستقيمين. الضلعين المتوازيين يسميان “القواعد”، بينما الضلعين الآخرين يُسميان “السيقان”. ويمكن حساب مساحة ومحيط شبه المنحرف بسهولة باستخدام علاقات رياضية بسيطة، حيث يتعين أيضًا حساب الارتفاع العمودي بين القواعد.
“شبه المنحرف” هو شكل هندسي أنيق وبسيط يستند إلى مفهوم الضلوع المتوازية والضلوع غير المتوازية. يتمتع هذا الشكل بقواعد متوازية ومسافة عمودية بينهما تُسمى الارتفاع. بفضل هذه البنية البسيطة، يمكن حساب مساحة الشكل ومحيطه بسهولة باستخدام العلاقات الرياضية البسيطة.
بالاستفادة من تلك الخصائص، يصبح شبه المنحرف أحد الأشكال الهندسية الأكثر فهمًا واستخدامًا في الرياضيات والهندسة. إذا كنت بحاجة إلى حساب مساحته أو محيطه، يمكنك الاعتماد على الصيغ والمعادلات البسيطة المتاحة لهذا الغرض، مما يجعل العملية سهلة وفعالة.
قد يهمك ايضاً : كيفية حساب الانحراف المعياري
خصائص شبه المنحرف
كل شكل هندسي له خصائص مميزة تميزه عن غيره، وفيما يتعلق بشبه المنحرف، إليك بعض من خصائصه المميزة:
- يتكون من 4 أضلاع، حيث اثنان منها متقابلان ومتوازيان ولكن بأطوال مختلفة، واثنان آخران متقابلان ومتساويان ولكن غير متوازيين.
- يتضمن 4 زوايا، حيث تكون زوايا القاعدتين متساويتين في القياس.
- يحتوي على قاعدة كبرى وقاعدة صغرى، وهما الضلعان المتوازيان اللذان يميزان هذا الشكل.
- يتمتع بقطرين متساويين يتقاطعان في نقطة واحدة وينصف كل منهما الآخر، مما يمنحه خصائص هندسية متميزة.
باختصار، شبه المنحرف يُميزه تواجده الفريد من الأضلاع المتوازية والزوايا المتساوية، مما يجعله شكلًا هندسيًا مثيرًا للاهتمام.
محيط شبه المنحرف
لحساب محيط شبه المنحرف بسهولة، يجب أولاً معرفة أطوال جميع أضلاع هذا الشكل. يتم ذلك من خلال تحديد طول القاعدتين والمستقيمين الآخرين. بعد ذلك، يمكنك حساب محيط شبه المنحرف بسهولة عن طريق جمع أطوال الأضلاع الأربعة معًا، وهذه العملية تُمثل في العلاقة التالية:
محيط شبه المنحرف = طول القاعدة الأولى + طول القاعدة الثانية + طول المستقيم الأول + طول المستقيم الثاني
يمكن قياس محيط شبه المنحرف باستخدام وحدات قياس مختلفة، مثل السنتيمتر أو المتر، وفقًا للمعايير المحلية واحتياجات الحساب.
مساحة شبه المنحرف
لحساب مساحة شبه المنحرف بسهولة، يتعين علينا أولاً معرفة طول كل من القاعدتين وأيضًا معرفة الارتفاع الخاص بالشبه المنحرف. يمكن التعبير عن مساحته على النحو التالي: تجميع طولي القاعدتين ومن ثم تقسيم الناتج على 2، وبعد ذلك ضرب النتيجة في الارتفاع. لذا، يُمكن صياغة القاعدة لحساب مساحة شبه المنحرف على النحو التالي:
مساحة شبه المنحرف = [ (طول القاعدة الأولى + طول القاعدة الثانية) / 2 ] × الارتفاع
باستخدام هذه الصيغة، يصبح حساب مساحة شبه المنحرف أمرًا بسيطًا وفعالًا.
خصائص الأشكال الرباعية
الأشكال الرباعية هي الأشكال الهندسية التي تتألف من أربعة أضلاع وأربعة زوايا. تتميز هذه الأشكال بخصائص مميزة تعرفها، وفيما يلي بعض الخصائص الشائعة للأشكال الرباعية:
- عدد الأضلاع: جميع الأشكال الرباعية تحتوي على أربعة أضلاع.
- عدد الزوايا: كل الأشكال الرباعية تحتوي على أربع زوايا.
- زوايا داخلية: إجمالي مقاييس زوايا أي شكل رباعي داخلياً يساوي 360 درجة. هذا ينطبق على جميع الأشكال الرباعية، بما في ذلك المربع والمستطيل والمربع والمنحرف.
- أضلاع متساوية: في المربع والمستطيل، تكون جميع الأضلاع متساوية في الطول.
- زوايا متساوية: في المربع والمستطيل، تكون جميع الزوايا متساوية في القياس.
- أضلاع متوازية: المستطيل والمربع هما أشكال رباعية تحتوي على أضلاعين متوازيين.
- زوايا قائمة: المربع يحتوي على أربع زوايا قائمة، حيث تكون قياساتها 90 درجة.
- شِقّات: الأشكال الرباعية يمكن أن تكون لها شِقّات، وهي مناطق داخلية محصورة بواسطة أضلاعها.
هذه بعض الخصائص الأساسية للأشكال الرباعية، وتختلف هذه الخصائص باختلاف نوع الشكل الرباعي.
في ختام هذا المقال، وبعد البحث والتفكير في السؤال المثير حول الشكل الرباعي الذي يحتوي على ضلعين فقط متوازيين، نجد أن هذا السؤال يمثل أحد تحديات الهندسة والرياضيات المثيرة. إن فهم الأشكال الهندسية وخصائصها يمكن أن يكون مثيرًا وممتعًا، ويفتح الأبواب أمام الاكتشاف والتفكير الإبداعي.
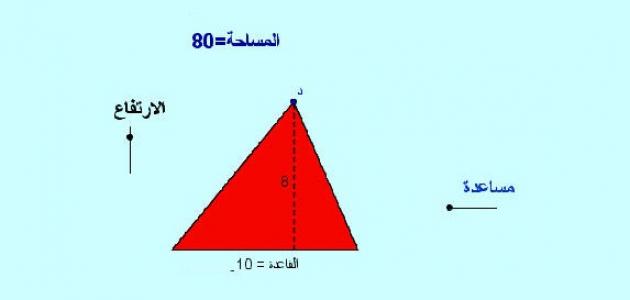
قد يهمك ايضاً : طريقة حساب مساحة المثلث