العبارات التي تمثل وحيدات حد هي : (بيت العلم)
يتم تعريف علم الجبر على أنه من ضمن أبرز فروع الرياضيات ، وهي قائم على مبدأ واحداً ألا وهو المعادلات التي تتألف من حزمة من المتغيرات والثوابت ، على أن تصبح الثوابت عبارة عن أعداد صاحبة قيمة معينة لا يمكن تغيرها ، منها على سبيل المثال العددين : 3، و14.98 عبارة عن قيم ثابتة ، أما بخصوص المتغير فيتم تعريفه على أنه عدد يمتلك قيمة ليست ثابتة ، وفي الغالب ما تستعمل أحرف اللغة من أجل التعبير عن تلك المتغيرات داخل المعادلات ، ومن الممكن أن تحتمل المتغيرات أكثر من قيمة واحدة ، وبمعادلات ثانية لا تمتلك إلا قيمة واحدة ، واليوم سوف نتعرف على إجابة سؤال يتكرر بكثرة في الجبر ألا وهم العبارات التي تمثل وحيدات حد هي : (بيت العلم).
العبارات التي تمثل وحيدات حد هي :
هذا السؤال دائماً ما يتكرر في اختبارات التلاميذ في مادة الرياضيات ، والإجابة الصحيحة هي :
- 22
- -13ب2
- ٣ب٣/س
- ٥ب٢/٣
- 6م + 3ن
- 23 أ ب د5ه
للمزيد يمكنك قراءة : في احدى الايام التي كان يوسف يراقب فيها
أهمية علم الجبر:
- قد يظن بعض الأشخاص بأن علم الجبر تنتهي أهميته عند انتهاء فترة الدراسة ، إلا أن هذا الاعتقاد خاطئ تماماً لأنه يشكل ركيزة من ركائز الحياة ، وذلك بداية من دفع إيصالات الدفع وإدارة الميزانيات.
- مروراً بتكاليف الرعاية الصحية حتى التخطيط للمشاريع القادمة ، إذ أن كل تلك الأشياء السابق ذكرها بحاجة لفهم أساسي لهذا العلم ، حيث ينطوي فهم ودراسة المفاهيم الرئيسية لهذا العلم على الكثير من الأشياء التي ترجع بالفائدة على الإنسان.
- وذلك لأنها تعمل على تطوير التفكير النقدي فضلاً للمنطق ومهارة حل الأزمات وتطوير مهارتي الاستدلال والاستنتاج ، والأبرز من هذا هو تطبيقات الحياة الحقيقية التي تكون بحاجة لمبادئ علم الجبر وأبرزها بمكان العمل.
فروع علم الجبر:
يتم تقسيم هذا العلم إلى الكثير من الأقسام الفرعية ، ومن أهمها ما يلي :
الجبر الابتدائي : ويسميه الكثير من الأشخاص (الجبر1) ، ويحتوي على المفاهيم التي تدخل بإطار الجبر الأولي التي منها على سبيل المثال : المتغيرات والمعادلات وخصائص المساواة وعدم المساواة ، فضلاً للمعادلات الجبرية وأيضاً المعادلات الخطية التي تضم متغير واحد أو اثنين ، والتعبير عن الكلمات من خلال الأعداد ، والعمليات الحسابية الـ4.
الجبر المتقدم : وهذا الفرع يسميه الكثير من الناس بـ(الجبر2) ؛ وهو عبارة عن المستوى المتوسط من علم الجبر الذي يمكنه أن يعالج ويتطرق لمستوى أكبر من المعادلات ، منه على سبيل المثال :
- المعادلات مع عدم المساواة
- التمثيل البياني للاقترانات والمعادلات الخطية.
- المقاطع المخروطية.
- معادلة كثيرة الحدود.
- المصفوفات.
- حلّ نظام المعادلات الخطية.
- علم المثلثات.
- الاقترانات التربيعية مع عدم المساواة.
- كثيرات الحدود والعبارات مع الجذور المتتاليات والمتسلسلات.
- التعابير العقلانية.
- الرياضيات المتقطعة والاحتمالات.
الجبر المجرد : وهو عبارة عن النوع أو الفرع الذي يختص بدراسة البنى والهياكل الجبرية التالي ذكرها :
- العمليات الثنائية : تعد الأساس لكافة الهياكل الجبرية ، فهي تتألف من حزمتين بمدخلاتها ، لينجم بسببها حزمة واحدة سهلة ومبسطة.
- المجموعات : ويتم إطلاقها على سلسلة من العناصر التي يجمعها خصائص شبيهة تكون هي المحدد والمميز للسلسلة.
- العنصر المحايد : وهما العددين واحد وصفر ، حيث يعد الـ0 هو العنصر المحايد لعملية الجمع ، والرقم واحد هو العنصر المحايد لعملية الضرب.
- العنصر المعاكس : وهو عكس العدد ولكن بإشارة سالبة بعملية الجمع ، وهو مقلوب الرقم بعملية الضرب.
- الترابطية : وتشير إلى تطابق عمليتين رياضيتين ، والمسألة التالية بإمكانها أن تسهل المفهوم أكثر : [(3 + 2) + 4 = 3 + (2 + 4)].
الجبر الخطي : وهو عبارة عن فرع من أفرع علم الجبر الذي ينطبق على كلاً من الرياضيات التطبيقية والبحتة ، ويتم استعماله في الكثير من المجالات ، وأبرزها ما يلي :
- المعادلات الخطية.
- مسافات المتجهات.
- العلاقات.
- المصفوفات وتحليلها.
الجبر التبادلي : وهو من ضمن أفرع علم الجبر التي تهتم بدراسة كل ما يتعلق بالحلقات التبادلية وهي عبارة عن الحلقات التي يصبح فيها الضرب تبادلي ، بمعنى : (a×b = b×a).
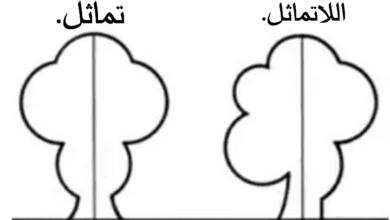
للمزيد يمكنك قراءة : خط تماثل ومحوره في الرياضيات للصف الرابع
مؤسس علم الجبر:
يعد محمد بن موسى الخوارزمي هو المؤسس لهذا العلم ، وقد بدأ الرجل مسيرته ببيت الحكمة في مدينة بغداد ، وعمل فيها في أول الأمر مترجم للنصوص الرياضية والفلكية التي كانت مكتوبة باللغة الهندية واليونانية للغة العربية ، وبعدها بمدة وجيزة حصل على ترقية وصار مدير لبيت الحكمة.
عمل الرجل في الترجمة جعله يطلع على كافة النظريات والقواعد المكتوبة ، وعرف بعدها أنه قد تكون هناك طريقة سهلة لحل المشاكل ، وقد اتبع بهذا نهجين اثنين أولهما هو التحول للنظام العددي الهندوسي الذي كان عبارة عن (1-9 و 0).
وهذا النظام بإمكانه تسهيل اللغة المستعملة لتسهيل المسائل ، أما النهج الثاني فكان تطوير طريقة أكثر شمولية من أجل تحليل المسائل بلغة رياضية ، وهو ما يطلق عليه اسم الجبر ، وقد أضاف العالم محمد بن موسى لعلم الجبر في سنة ثمانمائة وثلاثون ميلادياً 3 أساليب رئيسية يمكن من خلالهم حل المعادلات الرياضية المعقدة ، وهم كالتالي :
- الاختزال : ويشير إلى تسهيل كتابة العبارات الرياضية ، فضلاً لإعادة صياغتها بشكل يسير وسهل.
- الإكمال : ويشير لنقل الطرف السالب من أحد طرفي المسألة للناحية الأخرى ، فضلاً لقلب علامة الجانب الآخر، فلو كانت سالبة يتم قلبها لموجبة ولو كانت موجبة يتم قلبها لسالبة.
- الموازنة : وتشير إلى حل المسألة عن طريق إجراء عملية التساوي بين طرفي المعادلة.
للمزيد يمكنك قراءة : مربع العدد 8 يساوي! طريقة حساب مربع الأرقام