طول الضلع المجهول جـ في المثلث القائم يساوي؟ تعرف هنا ع الإجابة!
طول الضلع المجهول جـ في المثلث القائم يساوي
محتوي الموضوع
إن علم الرياضيات يعتبر من أفيد العلوم في الحياة ، وهذا العلم مهتم بدراسة كافة الأشكال الهندسية المتنوعة والمتعددة ، منها على سبيل المثال : المثلث والمربع والدائرة وغيرها الكثير ، ويعد المثلث واحداً من أبرز الأشكال الهندسية التي لديها علاقة وثيقة بالكثير من الأشكال الهندسية الأخرى ، وهناك أنواع للمثلث من جهة الزوايا ، على سبيل المثال : المثلث القائم الزاوية والثلث الحاد الزوايا والمنفرج ، وفي هذا اليوم سوف نقدم لكم طول الضلع المجهول جـ في المثلث القائم يساوي؟ تعرف هنا ع الإجابة!
طول الضلع المجهول ج في المثلث القائم:
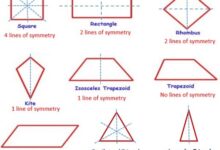
تبلغ زاوية المثلث القائمة تسعون درجة مئوية ، إذ أن المثلث مضلع ثلاثي منتظم يمتلك 3 أضلاع فضلاً لـ3 زوايا ، وهناك أنواع للمثلث من ناحية الزوايا منها ما هو حاد الزوايا ومنها ما هو قائم الزاوية ومنها ما هو منفرج.
- إذ أن المثلث القائم الزاوية يعتبر المثلث الذي فيه قياس أحد الزوايا تسعون درجة ، إذ أن مجموع قياسا زوايا أي مثلث تبلغ مائة وثمانون درجة ، وبخصوص السؤال الشهير في الرياضيات : طول الضلع الجهول ج في المثلث القائم يساوي؟
- الإجابة الصحيحة : إن طول الضلع المجهول ج في المثلث القائم يساوي تسعون درجة.
للمزيد من الأسئلة يمكنك قراءة : المفك هو رافعة من النوع
تعريف المثلث وخصائصه:
يُعرف المثلث بأنه صورة مغلقة ثنائية الأبعاد ، ومنها ما يكون ثلاثي الأبعاد كذلك ، ويتكون المثلث من 3 قطع مستقيمة الشكل ، تلك القطع تشكل الأبعاد تتقاطع بنهايتها حتى تكون رؤوس أو ما يطلق عليها زوايا ، ويسمى المثلث في الغالب وفق رؤوسه ، ويمتلك 3 زوايا يكون مجموع قياسها مائة وثمانون درجة ، ودوماً ما يواجه أو يقابل أقصر ضلع من المثلث أصغر زاوية داخلية ، ويواجه أطول ضلع من المثلث أكبر زاوية داخلية ، وفي الأسفل سوف نتعرف على أبرز المصطلحات التي تتعلق بالمثلث :
- القاعدة : من الممكن أن يشكل أي بعد من أبعاد المثلث قاعدة خاصة به ، إلا أنها في الغالب ما تكون البعد المرسوم بالأسفل ، وبالمثلث متساوي الساقين غالباً ما تكون القاعدة هي البعد غير المتساوي مع البعدين الآخرين ، ويتم استعمال القاعدة في معظم الأوقات من أجل حساب مساحة المثلث.
- الرأس : وهو عبارة عن زاوية المثلث ، ولدي كل مثلث 3 رؤوس.
- متوسط المثلث : وهو عبارة عن خط يمتد من رأس المثلث حتى منتصف الضلع الموازي له ، وإن لكل مثلث 3 منها وتتقاطع في نقطة واحدة فقط يطلق على هذه النقطة اسم النقطة المركزية للمثلث.
- الارتفاع : وهو عبارة عن العمود الذي يمتد من القاعدة حتى رأس المثلث الموازي له ، وبما أنه يوجد 3 قواعد محتملة للمثلث فإنه يوجد 3 ارتفاعاته محتملة كذلك ، وتتقاطع بنقطة يطلق عليها اسم ملتقى الارتفاعات أو المركز القائم.
خصائص المثلث:
من أبرز خصائص المثلث بالإضافة لما ذكرناه التالي :
- لو وازى مستقيم أحد أبعاد المثلث وقطع البعدين الآخرين فإنه يتم تقسيم المثلث إلى مثلثات شبيهة ومتوافقة بالطول.
- مجموع أطوال أي بُعدين من المثلث أكبر من طول البعد الثالث في الغالب ، وبالمثل الفرق ما بين أطوال أي بعدين يكون أقل من طول البعد الثالث في الغالب.
- إن الزاوية الخارجية للمثلث تعادل أو تساوي مجموع الزاويا الداخلية التي تقابلها أو التي تبعد عنها ، ويكون مجموع الزوايا الخارجية للمثلث هو ثلاثمائة وستون درجة.
- يتم تقسيم ارتفاع المثلث الذي يكون متساوي الساقين والمثلث متساوي الأبعاد القاعدة لنصفين متعادلين ، كما يتم تقسين المثلث لمثلثين متساويين.
للمزيد من الأسئلة يمكنك قراءة : من الأسماء الموصولة المشتركة هي …… شرح مبسط للاطفال
أنواع المثلثات وفق طول الأبعاد:
نستطيع أن نقسم المثلثات وفق طول الأبعاد كما في التالي :
- المثلث متساوي الأبعاد : وهو عبارة عن مثلث يمتلك 3 أبعاد متساوية بالطول و3 زوايا متساوية قياس كل منها ستون درجة.
- المثلث متساوي الساقين : وهو عبارة عن مثلث يمتلك بعدين متساويين بالطول ، وزاويتين متساويتين بالقياس ويطلق عليها اسم زاويتا القاعدة.
- المثلث مختلف الأبعاد : وهو عبارة عن مثلث لا يمتلك أي أبعاد متساوية بالطول ، أو زوايا متساوية بالقياس.
أنواع المثلثات وفق الزوايا:
نستطيع أن نقسم المثلثات وفق الزوايا التي تحتويها كما في التالي :
- المثلث حاد الزاويا : وهو عبارة عن مثلث يكون قياس كل زاوية من زواياه أقل من تسعون درجة.
- المثلث قائم الزاوية : وهو عبارة عن مثلث لديه زاوية قائمة قياسها تسعون درجة.
- المثلث منفرج الزاوية : وهو عبارة عن مثلث لديه زاوية منفرجة قياسها أكبر من تسعون درجة.
بعض الملاحظات الهامة للغاية:
- في بعض الحالات من الممكن أن يكون لدى المثلث اسمين ، فعلى سبيل المثال : من الممكن أن يكون المثلث قائم الزاوية ومتساوي الساقين في ذات الوقت ، وذلك نتيجة لامتلاكه لزاوية قائمة وبُعدين متساويين من ناحية القياس.
- تسمى أبعاد المثلث قائم الزاوية أسماء خاصة به ، فالبعد المقابل للزاوية القائمة يطلق عليه اسم الوتر ، أما بخصوص البعدين الآخران فيطلق عليهما اسم الساقين.
- من الممكن استعمال نظرية فيثاغورس من أجل إيجاد أطوال أبعاد المثلث قائم الزاوية ، إذ أن مربع الوتر يساوي مجموع مربعي البعدين الآخرين ، ويتم التعبير عن تلك النظرية بالقانون الشهير ألا وهو : (الوتر)²=(الضلع الأول)²+(الضلع الثاني)².
- إن الارتفاع بالمثلث قائم الزاوية يعد أحد البعدين المتعامدين على البعد الآخر ، وبحال اعتبار أحدهما هو الارتفاع فإن البعد الآخر العمودي عليه يعتبر قاعدة هذا المثلث.
للمزيد من الأسئلة يمكنك قراءة : اي مما يلي من خصائص الفلزات