محتوي الموضوع
الكرة من الاشكال المعروفه في حياتنا اليومية, فنجد العديد من الاشكال والمجسمات الكروية ,مثل الكرة الارضية وكرة القدم ,وياتي مركز الكرة من نقطة داخلية تقع في المنتصف, وتبعد جميع النقط بالتساوي عن مركز الكرة ,ويمكن حساب نصف قطر الكرة بالبعد بين اي نقطة علي سطح الكرة, ومركز الكرة والكرة هي المحل الهندسي لمجموعة من النقاط.
الكرة من المجسمات الثلاثية الابعاد و الثنائية الابعاد, حيث تدخل في الاشكال الهندسية ويعتبر اقرب شكل لها هو الدائرة , يمكن حساب مساحة وحجم ومحيط الدائرة مثلها مثل باقي الاشكال الهندسية ,وحيث انها جسمها كروي فتحسب مساحة الكرة بعدد السنتيمترات التي تغطي السطح الخارجي للكرة, وقد تم اكتشاف معادلة مساحة الكرة من قبل عالم الرياضيات الشهير ارسطو ,وهي=(4ط نق2) حيث ان (ط )هو عدد طبيعي معلوم ونق هي نصف قطر الدائرة
الكرة مثل باقي الاشكال الهندسية يمكن حساب حجمها, وهي القطعة المستقيمة التي تصل بين اي نقطتين على سطح الكرة ,و تمر بمركز الكرة ونستنتج من ذلك لحساب حجم الكرة او الدائرة ,يجب حساب نصف قطرها وهو 4/3 ط نق3.
أقراء ايضا:ما هو محيط المستطيل بقانون المساحة والعرض

مساحة سطح الكرة
تتسم الاشكال الكروية بمساحة سطح اصغر من باقي الاشكال الهندسية, لحساب مساحة سطح الدائرة يجب تطبيق القانون الخاص بحساب مساحة سطح الكرة والدائرة وهو:
مساحة السطح = 4 × ط × نق2
- نق هو نصف قطر الكرة :” و هو المسافة من مركز الكرة إلى سطحها.
- ط أو “باي:” وهو يساوي 3.14 تقريبًا هو رمز ثابت يستخدم في كل المعادلات ,وهي نسبه تحسب بين محيط الدائرة وقطرها
كيفية حساب نصف قطر الكرة. قد يكون من معطيات المسالة او مجهول ,ولكن يمكن حسابها بعده طرق :
- الطريقة الاولي هي بقسمة حجم الكرة الي 4, والضرب في العدد الثابت (ط) حيث تقدر بقيمة =3.14اواستخدام الالة الحاسبة وهو موجود بالرمز (π) ,وضرب الناتج في 3 ثم حساب الجذر التكعيبي.
- بطريقة الثانية :وهي بالبعد بين اي نقطة علي سطح الكرة.
- الطريقة الثالثة: قسمة القطر علي 2.
ولحساب الأس التربيعي لنصف القطر يكون ذلك بضرب القيمة في نفسها .
أمثلة محلولة علي حساب مساحة سطح الكرة
مثال (1)
كم مساحة سطح كرة قيمة نصف قطرها 8 سنتيمتر؟
الحل :
- مساحة السطح = 4 × ط × نق2
- نق = 8.
- 4 × ط × 2.8
- 64 × 4 × ط.
- 256 × ط.
- مساحة السطح = 803.84 سم2، أو 803.84 سنتيمتر مربع.
مثال ( 2 )
احسب مساحة سطح كرة إذا كان قطرها يبلغ 10 سم .
الحل :
نق ( طول نصف قطر الكرة ) = 10\2 = 5 سم .
مساحة سطح الكرة = 4 ط نق 2
مساحة سطح الكرة = 4 × 22/5 × ( 5×5) = 4 × 22\5 × 25 = 314 سم2 .
مثال ( 3 )
كرة يبلغ حجمها 4300\3 سم3 اوجد طول نصف قطرها .
الحل :
حجم الكرة = 4/3 ط نق3 .
4312\3 = 4\3 X 22\7 X نق3 .
نق3 = 4300 \3 X 3\4 X 7\22 = 4300 X 3 X 7 \ 3 X4 X 22 = 343 .
نق = الجذر التكعيبي لـ 342 = 7 سم .
مثال ( 4 )
كرة تبلغ مساحة سطحها 1200 سم2 , اوجد طول نصف قطرها .
الحل :
مساحة سطح الكرة = 4ط نق2 .
1200 = 4 × 3.14 نق2 .
نق2 = 1200 \ ( 4 × 3.14 ) =95.5 .
نق = الجذر التربيعي لـ95.5 = 9.77 =10 سم
أقراء ايضا:تشخيص صعوبات التعلم وأسبابها وعلاجها
حساب حجم الكرة
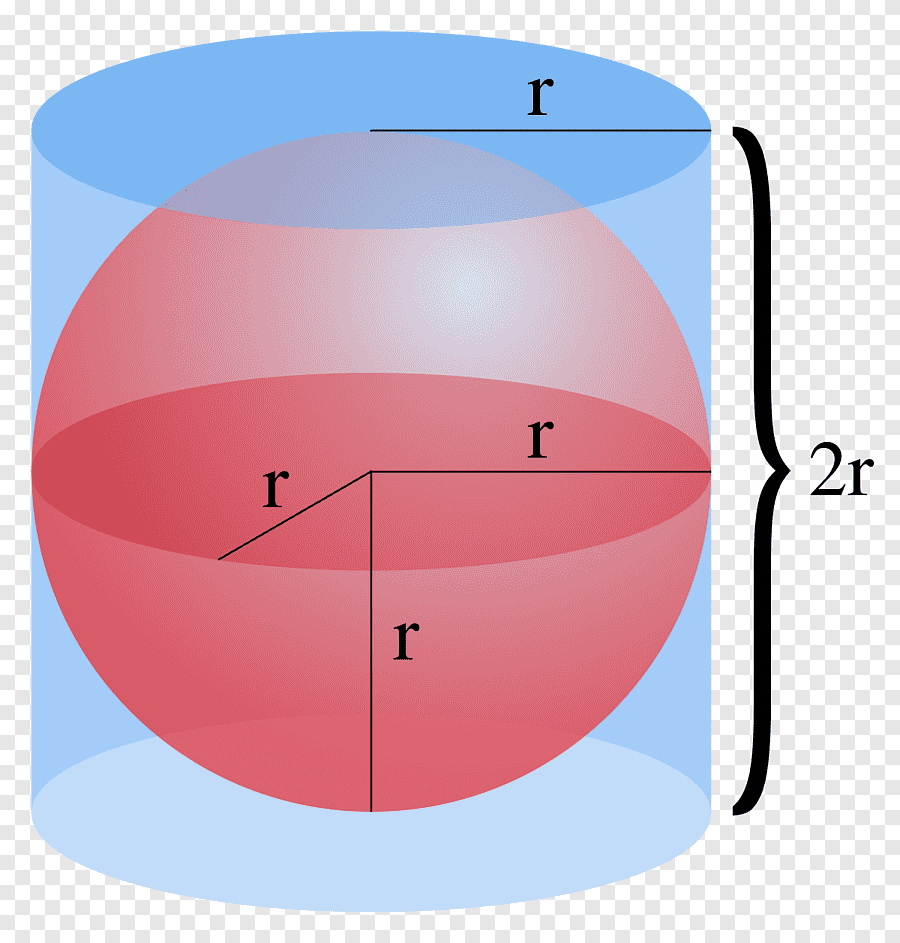
لحساب حجم كرة يجب معرفة نصف قطر الكرة ,وذلك عندما يكون حجم الكرة مجهولا, وذلك من خلال المعادلة ح = 4/3 ط نق3,حيث (ح) حجم الكرة ,ولحساب حجم جزء معين من الكرة يجب حساب الحجم الكلي للكرة ,ثم الضرب في الجزء الذي تريده,اي عند حساب حجم نصف الكرة ,نحساب حجم الكرة الكلي ثم نضرب في نصف 0.5 وهكذا.
قانون حساب حجم الكرة ح = 4/3 ط نق3 يتكون القانون من تكعيب نصف القطر و(ط) والرقم الثابت 4/3
أقراء ايضا:طريقة سهلة للقسمة شرح بسيط للطلاب
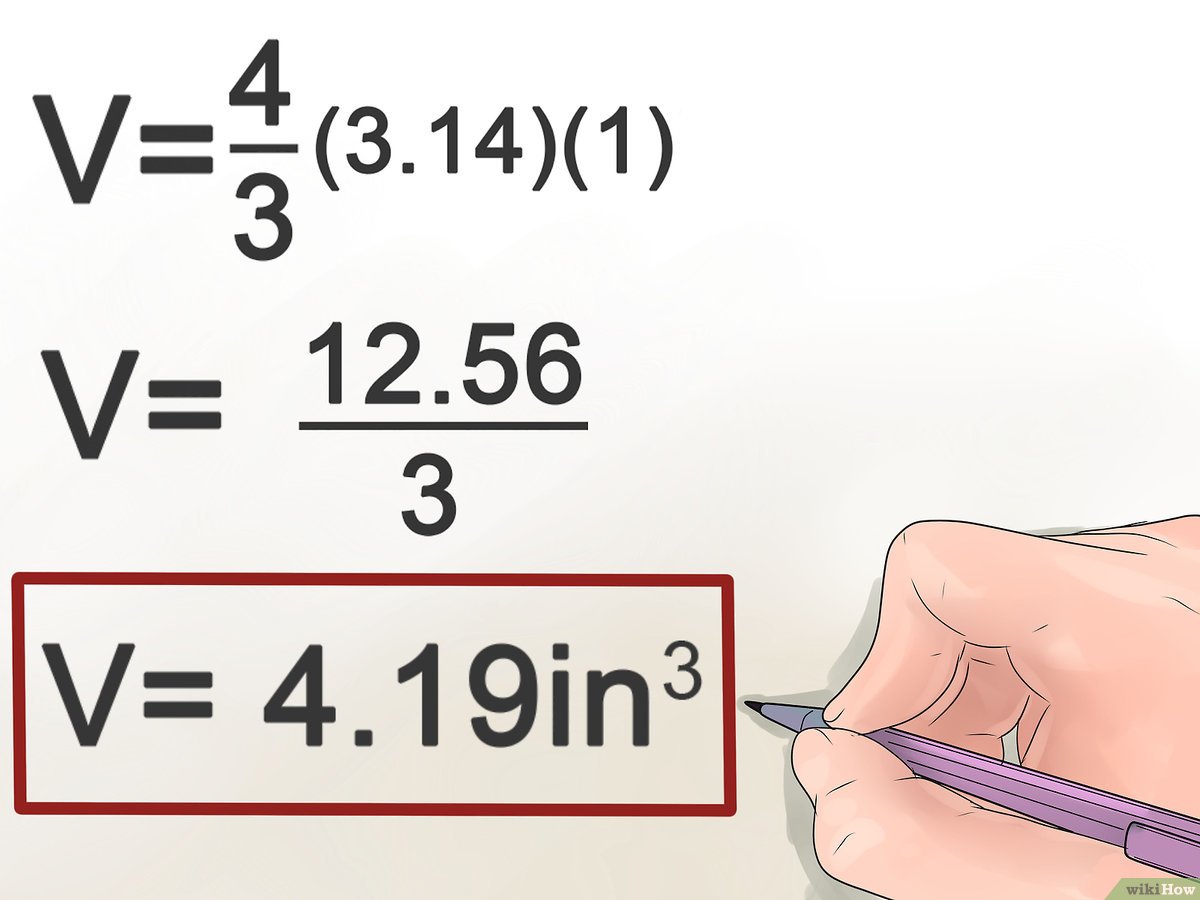
أمثلة محلولة علي حساب حجم الكرة
حجم الكرة .
يتم حساب حجم الكرة من خلال القانون:حجم الكرة = 4/3 ط نق3 .
مثال ( 1 )
احسب حجم كرة ، نصف قطرها4 سم .
الحل :
حجم الكرة = 4/3 ط نق3
حجم الكرة = 4/3 × 3.14 × ( 4 )3 = 4/3×803.4
مثال (2 )
إذا كان لدينا كرة طول قطرها يساوي 10 سم, المطلوب مساحة سطح الكرة وحجمها .
الحل:
طول نصف قطر الكرة = 10\2 = 5 سم .
مساحة سطح الكرة = 4 ط نق2 .
مساحة سطح الكرة = 315 سم2 .
حجم الكرة = 4/3 ط نق3 .
حجم الكرة = 523سم3 .
أقراء ايضا:ما هو قانون مساحة المستطيل ومحيطه وأقطاره